Уравнение для расчета простого трубопровода

По самому определению простого трубопровода жидкость движется в нём из-за разности потенциальных энергий в начале и в конце его - поэтому при его расчете обязательно должны присутствовать параметры, характеризующие потенциальную энергию (напор или давление) и параметры течения, скорость или расход. Ясно, что основным уравнением, связывающим потенциальную и кинетическую энергии, является уравнение Бернулли.

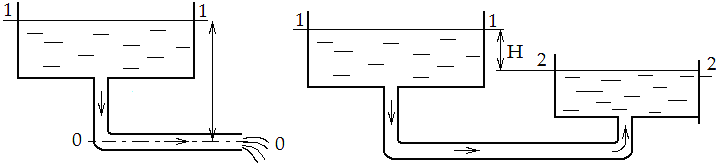
Большинство простых трубопроводов вписывается в одну из следующих схем (рис. 11.1); в резервуарах уровень поддерживается постоянным и поэтому течение везде установившееся.

В обоих случаях движущей силой является сила тяжести, которая приводит к разности давлений и под действием этой разности жидкость приходит в движение. В обоих случаях потенциальная энергия положения преобразуется в кинетическую энергию, а последняя - в тепловую за счет сил трения.

Основные расчетные зависимости могут быть получены применением уравнения Бернулли к сечениям 1-1 и 2-2; как следует из рис. 11.1, ось сравнения выбрана совпадающей с осью горизонтальной части трубопровода, а сечения 1-1 и 2-2 совпадающими со свободными поверхностями в сосудах. Суммарные потери h_Σ складываются из потерь по длине h_l и местных h_м

h_Σ=h_l+ h_м (11.1)

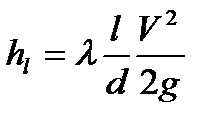и .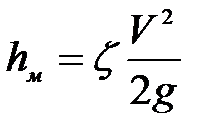

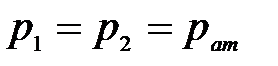
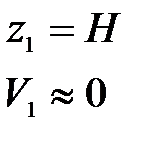
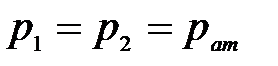
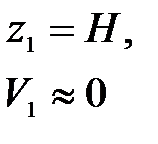
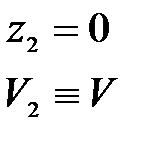
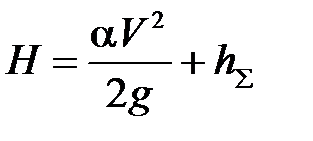
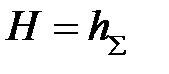
Схема 1 Схема 2

Рис. 11.1

Физический смысл уравнения для схемы 1

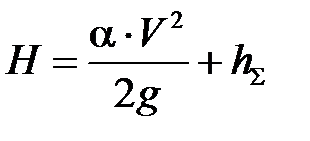(11.2)

следующий: потенциальная энергия положения преобразуется в кинетическую энергию движущейся жидкости, которая частично превращается в тепло. Для схемы 2 имеем

Н= h_Σ, (11.3)

т.е. вся потенциальная энергия полностью преобразуется в тепло.

Уравнение (11.2) может быть преобразовано так

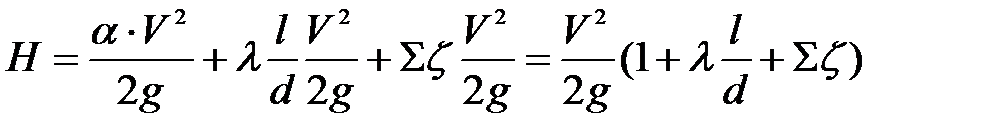
(приняли, что α ≈ 1).

Уравнения (11.2) и (11.3) для обеих схем имеют одинаковый вид, а именно

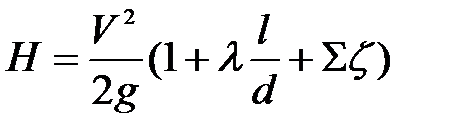(11.4)

(для схемы 2 из всей суммы коэффициентов местных сопротивлений выделяется коэффициент для внезапного расширения при входе трубы в емкость 2 - он равен единице, т.е 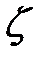=1).

Если труба круглая, то средняя скорость выражается так

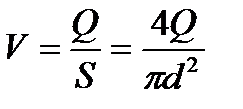(11.5)

и уравнение (11.4) преобразуется с учётом (11.5) к виду

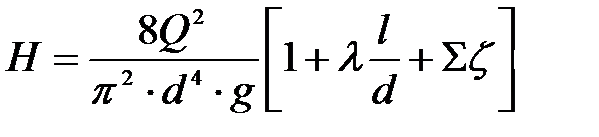. (11.6)

Это уравнение будем в дальнейшем называть основным уравнением для расчета простого трубопровода.

В случае, если простым трубопроводом является труба с несколькими местными сопротивлениями на ней (рис. 11.2), то, применяя к начальному 1-1 и конечному сечениям уравнение Бернулли, получим

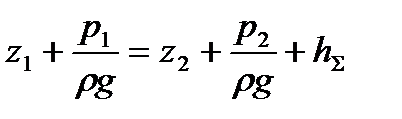. (11.7)

Величины z₁ и z₂ всегда могут быть учтены, поэтому их вообще здесь не принимаем во внимание. Уравнение (11.7) можно представить как в терминах напоров

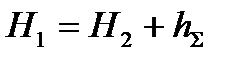(где 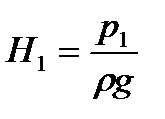, 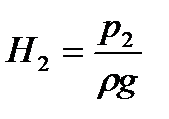), (11.8)

так и в форме давлений (после умножения обеих частей на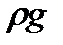

Рис. 11.2

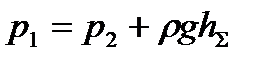. (11.9)

Последнее уравнение (11.9) приводится к виду

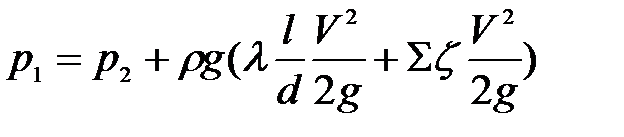
или

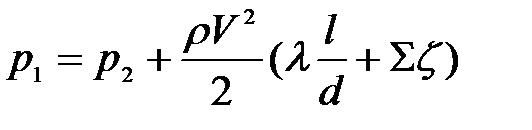. (11.10)

Если учесть, что в случае круглой трубы

,

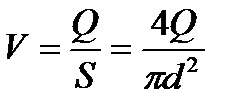то (11.10) запишется в виде

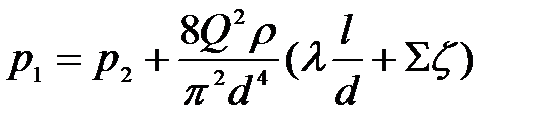. (11.11)

Уравнение (11.11) принципиально не отличается от (11.6) и имеет простой физический смысл: потенциальная энергия убывает вдоль потока за счет потерь напора (кинетическая энергия остается постоянной).

Дата добавления: 2015-05-10