Ряды динамики, их виды, порядок построения

Тема 1.5 Ряды динамики

1.Ряды динамики, их виды, порядок построения

2.Показатели ряда динамики: уровень, абсолютный прирост, темп роста, темп прироста, абсолютное значение одного процента прироста

3.Средние показатели рядов динамики и методика их расчета

Одной из важнейших задач статистики является изуче­ние развития явлений общественной жизни во времени. Эта задача решается посредством построения и анализа статисти­ческих рядов динамики.

Рядами динамики в статистике называются ряды рас­положенных в хронологическом порядке показателей, ха­рактеризующих изменение величины общественных явле­ний во времени.

Ряды динамики состоят из числовых значений двух пока­зателей: моментов или периодов времени t, ккоторым отно­сятся приводимые данные, и соответствующих им статисти­ческих данных у, которые называются уровнями динамичес­кого ряда.

В зависимости от того, к моментам или периодам времени привязываются статистические данные, различают два вида рядов динамики:

– моментные;

– интервальные.

Если уровни ряда динамики выражают состояние явления на определенные моменты времени или даты, то такие ряды называют моментными рядами динамики.

Особенность моментного ряда динамики в том, что неко­торые его уровни содержат элементы повторного счета, т. е. каждый последующий уровень полностью или частично вклю­чает в себя предыдущий уровень. Поэтому суммирование уров­ней моментного динамического ряда не имеет смысла, но раз­ность уровней имеет определенное значение. Например, пока­зывает увеличение или уменьшение величины показателей за период между моментами или датами их учета.

Когда уровни ряда динамики характеризуют размеры об­щественных явлений за определенные интервалы (периоды) времени (за сутки, месяц, квартал, год и т. п.), то такие ряды называются интервальными (или периодическими).

В отличие от моментного ряда динамики, уровни интер­вального ряда динамики могут быть суммированы. Напри­мер, сложив данные выпуска станков за четыре квартала, можно получить показатель их выпуска за год. Это свойство интер­вальных рядов положено в основу построения статистичес­кой отчетности, когда показатели записываются нарастающим итогом с начала отчетного месяца или квартала.

По полноте, с которой отражается период времени, как в моментных, так и в интервальных рядах динамики, их делят на два вида:

–полные;

–неполные.

В полных рядах динамики одноимен­ные моменты или периоды времени строго следуют один за другим в календарном порядке, а в неполных рядах нет такой строгой хронологической последовательности.

Полные ряды называют рядами динамики с равноотстоящими уровнями,а неполные– с неравноотстоящими уровнями.

В зависимости от вида статистических показателей, исполь­зуемых при изучении явления, ряды динамики подразделяют­ся на три вида:

– ряды динамики абсолютных величин;

– относительных величин;

– сред­них величин.

Исходными, первоначальными являются ряды динамики абсолютных величии, так как их получают непос­редственно при сводке материалов статистического наблюде­ния.

Ряды динамики относительных и средних величии явля­ются производными рядами.

Рядами динамики относитель­ных величин являются ряды показателей, характеризующих темпы динамики изучаемого явления, изменение его структу­ры, интенсивности и т. п.

Рядами динамики средних вели­чин называются ряды показателей, которые выражают средние значе­ния изучаемого явления за определенные промежутки време­ни: среднюю выработку продукции на одного работающего, среднюю заработную плату, среднюю урожайность и т. п.

Если ряды динамики представлены относительными или средними величинами, их суммирование не имеет смысла. Ряды ди­намики относительных и средних величин используются для характеристики качественных изменений экономики.

2.Показатели ряда динамики: уровень, абсолютный прирост, темп роста, темп прироста, абсолютное значение одного процента прироста

При изучении динамики социально-экономических явле­ний рассчитывают аналитические показатели:

–абсолютные приросты;

–темпы роста и прироста;

–абсолютное значение одного процента прироста (снижения).

Расчет этих показа­телей основан на абсолютном или относительном сравнении уровней динамического ряда. При этом сравниваемый уро­вень называется текущим, а тот уровень, с которым сравнива­ют, базисным. За базисный уровень обычно принимается либо предыдущий уровень, либо начальный (первый) в дан­ном динамическом ряду.

Если сравнивается каждый последующий уровень с предыдущим, получают цепные показатели динамики. Если каждый уровень сравнивается с начальным или каким-либо другим, принятым за постоянную базу сравнения, получают базисные показатели динамики.

Абсолютный прирост – это разность двух уровней ряда динамики. Он показывает, на сколько единиц данный уровень больше или меньше уровня, взятого для сравнения, и выражается в тех же единицах, что и уровни динамического ряда.

Цепной абсолютный прирост ∆у_ц исчисляется как разность между сравниваемым (текущим) уровнем у_i и уровнем, который ему предшествует у_i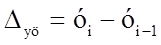-1

(1)

у_i-1 - предшествующий уровень ряда.

Базисный абсолютный прирост ∆у_б исчисляется как разность между сравниваемым уровнем у_i и уровнем, принятым за постоянную базу сравнения у_о

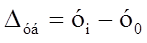(2)

где у_о - уровень, принятый за постоянную базу сравнения.

Абсолютный прирост может иметь и отрицательный знак, показывающий, насколько уровень изучаемого периода ниже базисного.

Сумма цепных абсолютных приростов за определенный период времени равна базисному абсолютному приросту за весь этот период.

Темп роста – это отношение двух уровней ряда динамики. Он показывает, во сколько раз больше (или меньше) или сколько процентов данный уровень составляет по отношению к другому уровню, взятому для сравнения. В первом случае темп роста выражается в коэффициентах, во втором – в процентах.

Цепной темп роста Тц исчисляется как отношение между сравниваемым (текущим) у_iуровнем и предшествующим ему уровнем

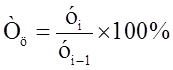или (3)

Базисный темп роста Т_б исчисляется как отношение между сравниваемым уровнем у_iи уровнем, принятым за постоянную базу сравнения у_о

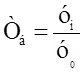или (4)

Если темп роста меньше единицы, то имеет место не рост, а снижение (падение) анализируемого уровня.

Последовательное произведение цепных темпов роста, выраженных в коэффициентах, за определенный период времени дает базисный темп роста за этот же период.

Отношение анализируемого базисного темпа роста к предыдущему дает соответствующий цепной темп роста.

Темп прироста ∆Т - это отношение абсолютного прироста к уровню, принятому за базу сравнения. Если он выражается в процентах, то показывает, на сколько процентов уровень данного периода больше (меньше) базисного.

Цепной темп прироста ∆Тц исчисляется как отношение цепного абсолютного прироста ∆Уц к предыдущему уровню ∆У_i-1

(5)

Базисный темп прироста ∆Т_б исчисляется как отношение базисного абсолютного прироста ∆У_б к базисному уровню У_о

(6)

Темп прироста, выраженный в процентах, вычисляется по формуле

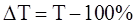(7)

Темп прироста может быть как положительной, так и отрицательной величиной. В первом случае это свидетельствует о положительной динамике (росте), а во втором – об отрицательной динамике (снижении).

Абсолютное значение 1% прироста Аi% - это отношение абсолютного прироста ∆У_i за определенный период к темпу прироста ∆Т_i за этот же период, выраженному в процентах.

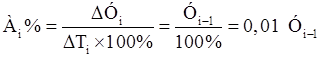(8)

Выражается Аi% в единицах измерения уровней анализируемого ряда динамики.

Дата добавления: 2015-05-10