Математическая обработка двойных, некоррелированныхых, равноточных измерений «n» различных величин

Математическая обработка повторных измерений.

В практической деятельности часто приходится иметь дело с повторными измерениями, выполняемыми с целью контроля качества наблюдений, с целью мониторинга физического состояния объекта, с целью повышения точности окончательных результатов, а чаще всего с целью одновременного решения указанных и подобных этим задач. Такие наблюдения, естественно, разделены во времени. Если такое разделение незначительно, то мы в праве предположить, что наблюдаемые объекты не претерпели изменений своих геометрических параметров. Когда же повторные измерения значительно разделены во времени, мы не можем быть уверены в стабильности наблюдаемых параметров. Кроме того, технологии, использовавшиеся при первичных и повторных наблюдениях, могут отличаться по точности, продолжительности и/или по стоимости. Дополнительно отметим, что результаты первичных и повторных наблюдений могли быть подвергнуты на своём этапе МНК-опимизации (уравниванию).

Всё выше сказанное говорит о том, что проблема математической обработки повторных наблюдений может быть разбита на решение близких, но различных задач, акценты в которых будут варьироваться.

Основных вопросов будет три:

ü нахождение наиболее надёжных значений (ННЗ) измеренных величин;

ü оценка точности (ОТ) измерений и проверка гипотезы (ПГ) о незн а чимости средней разности технологий первичных и повторных измерений;

ü ОТ ННЗ измеряемых величин.

Для начала рассмотрим два простейших случая обработки и анализа некоррелированных повторных измерений, выполненных для «n» различных величин.

Выполним постановку задач, определённых выше.

Дано:

Числовая информация:

x₁, x₂, …, x_n – ряд первичных измерений;

x´₁, x´₂, …, x´_n – ряд повторных измерений тех же величин;

n – количество измеряемых величин.

Теоретические посылки:

X _i – реальные значения измеряемых величин; i = 1, 2, …, n;

Х_i и Х΄_i – случайные величины (СВ), представляющие собой вероятностные модели первичной и повторной измерительных технологий, некоррелированных между собой (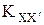 = 0_nn);

x_i 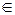X_i и x_í 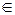X_í - i-ые результаты первичных и повторных измерений, трактуемые как элементы спектров СВ X_i и X_i ́, каждая из которых является компонентом своего вектора «X_n1» или «X′_n1»;

E(X_i) и E(X_í) – МО вероятностных моделей Х_i и X_í;

E(X_i) = E(X_í) = X_i – предположение об отсутствии постоянных ошибок в каждой из технологий;

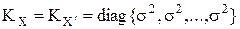– ковариационные матрицы измерений, отражающие некоррелированность и равноточность данных внутри каждой технологии.

Найти:

1) 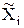- ННЗ измеряемых величин;

2) 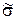- ОТ измерений и проверить гипотезу о незн а чимости различия технологий первичных и повторных измерений;

3) 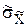- ОТ ННЗ измеряемых величин.

Решение:

1. Нахождение ННЗ измеряемых величин.

Каждая величина X_i измерялась дважды: x_i и x_í́. Эти измерения не коррелированы и равноточны. Следовательно, ННЗ результатов таких измерений будет среднее арифметическое соответствующей пары:

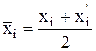. (D.1)

2. ОТ измерений и ПГ о незн а чимости различия технологий.

Оценка точности измерений производится по их разностям

d_i = x_i - x_í, (D.2)

совокупность которых

d₁, d₂, …, d_n (D.3)

образует ряд некоррелированных равноточных величин.

На основании формулы оценки точности ряда некоррелированных равноточных величин (Q.5), мы можем сразу найти СКО разностей:

m_d 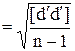, (D.4)

где d΄ = d - 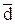- это разности, исправленные на величину

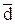= [d] / n, (D.5)

являющуюся средним арифметическим всех разностей обеих технологий и представляющей собой ОФ математического ожидания разностей

E(D_n1) = E(X_n1) – E(X΄_n1). (D.6)

Предположив отсутствие постоянной разности технологий, что отражено в «Теоретических посылках», получим предположение

E(D_n1) = 0, (D.7)

гипотезу о котором

H₀ = { E(D_n1) = 0} (D.8)

необходимо проверить против альтернативной

H_A = { E(D_n1) ≠ 0}. (D.9)

Проверка гипотезы (D.8) осуществляется по методике, рассмотренной в разделе «Вероятностное моделирование ошибок измерений», где проверялась гипотеза о равенстве среднего арифметического значения стохастически не связанных, равноточных измерений номиналу эталона.

В качестве теста вычисляется величина

t_Э = 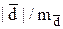. (D.10)

СКП среднего значения разностей – это СКП среднего арифметического:

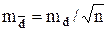(D.11)

Критическая область проверяемой гипотезы находится за пределами интервала t_T = [t_H; t_B], нижняя t_H и верхняя t_B границы которого – это квантили распределения Стьюдента, определяемые при (n – 1) степени свободы на уровне значимости a:

t_H = - t_B; t_B = t_n-1;a. (D.12)

Когда t_Э 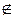t_T, нулевая гипотеза отвергается, т.е. среднее значение разностей (D.5) признаётся знáчимым и должно учитываться в формуле оценки точности разностей (D.4).

Отвергая нулевую гипотезу, мы признаём знáчимой разницу используемых технологий и должны принять соответствующее решение о них как в точностном, так и в стоимостном отношении.

Если же t_Э 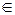t_T, то нулевая гипотеза не отвергается, а СКП разностей принимает вид

m_d 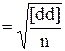. (D.13)

В такой ситуации разности d_i = x_i - x_í́ – это уклонения от E(D_n1) = 0 и знаменатель формулы для m _d не должен учитывать потерю информации, связанную с оценкой среднего значения разностей.

Итак, оценив точность разностей по формулам (D.4) или (D.13), мы можем приступить к оценке точности измерений x_i и x_í́, используя соотношение (D.2), из которого следует (в силу предполагаемой равноточности технологий), что

m_d² = m_x² + m_x² = 2m_x². (D.14)

Далее получаем обратное соотношение

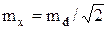. (D.15)

Окончательно, используя выражения (D.4), (D.13) и (D.15), имеем два варианта оценки точности измерений по их разностям:

с учётом среднего значения разностей - 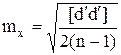(D.16)

и без учёта среднего значения разностей - 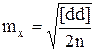. (D.17)

3. ОТ ННЗ измеряемых величин.

Поскольку ННЗ измеряемых величин – это средние арифметические двойных некоррелированных, равноточных результатов, то, опираясь на соотношения (D.1) и (D.15), мы можем сразу записать общее решение

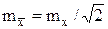, (D.18)

а с учётом (D.16) и (D.17) два различных:

с учётом среднего значения разностей - 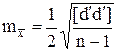(D.19)

и без учёта среднего значения разностей - 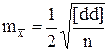. (D.20)

Дата добавления: 2015-05-10