Кинематика теории относительности

(следствия из преобразований Лоренца).

Рассмотрим некоторые результаты, получаемые в кинематике теории относительности. Они, как мы увидим, вытекают из преобразований Лоренца.

1. Предельный характер величины скорости света.

В классической механике считалось, что тела могут двигаться с любыми сколь угодно большими скоростями. Однако из преобразований Лоренца следует, что относительные скорости тел имеют верхнюю границу.

При переходе от неподвижной системы отсчета К к движущейся системе отсчета К’ преобразования Лоренца для координат и времени имеют вид:

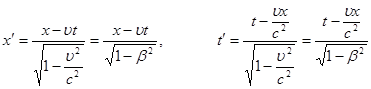(1)

Здесь мы ввели для удобства записи формул обозначение .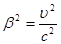

Координата и время не могут быть мнимыми. Поэтому подкоренное выражение должно быть больше нуля, а u/c<1, то есть u<c.

Следовательно, скорость v относительного движения двух инерциальных систем отсчета не может превосходить скорость света в вакууме.

2. Нарушение одновременности удаленных событий.

Пусть в системе К в точках с координатами x₁ и x₂ происходят одновременно два события в момент времени t₁=t₂=t₀. Тогда для наблюдателя находящегося в системе К’, движущейся со скоростью u относительно системы К, времена будут разные:

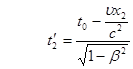(2)

Из этих формул видно, что .

Если же x₁=x₂, то . То есть события, происходящие одновременно в одном месте в системе К будут совпадать в пространстве и времени и в системе К’. Для удаленных точек одновременность нарушается.

3. Длительность событий в разных системах.

Предположим, что в некоторой точке А с координатой x в системе К происходит некоторое событие, длительность которого равна

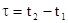
где t₁ – момент начала события, t₂ – момент окончания события.

Чему будет равна длительность этого события для наблюдателя находящегося в системе К’?

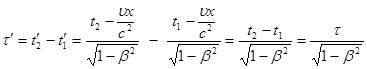
(3)

Отсюда видно, что длительность события, происходящего в некоторой точке А, минимальна в той инерциальной системе отсчета, относительно которой точка А неподвижна.

Время t, отсчитанное по часам, находящимся в той системе, относительно которой точка А неподвижна, (или иначе говорят, по часам движущимся вместе с телом) называется собственным временем этой системы. Как видно из полученной формулы , собственное время всегда меньше, чем время, отсчитанное по часам в движущейся системе отсчета.

Этот релятивистский эффект замедления времени получил непосредственное подтверждение в опытах с m-мезонами, элементарными частицами, входящими в состав космических лучей. Они быстро распадаются, среднее время жизни неподвижного m-мезона равно 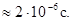Мезоны возникают в атмосфере на высоте 20-30 км и значительном количестве достигают поверхности Земли. Но исходя из времени жизни 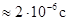мезон даже двигаясь со скоростью света мог бы пролететь всего . Чем же объяснить, что они достигают поверхности Земли? 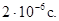- это время жизни неподвижного мезона. Если он двигается, то в системе отсчета движущейся вместе с ним он будет оставаться неподвижным и время его жизни будет тем же самым, то есть 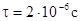- это собственное время жизни мезона. Время же по часам экспериментатора, связанного с Землей, оказывается гораздо больше, . Так как скорость мезонов близка к скорости света, то и за это время они успевают достигнуть поверхности Земли.

Вследствие релятивистского эффекта замедления времени и на космическом корабле течение времени должно замедляться. Поэтому длительность космического полета по часам космонавтов будет меньше длительности этого полета, измеренного по часам на Земле. Но этот эффект может оказаться значительным и наблюдаемым только если удастся осуществить полеты космических кораблей со скоростями близкими к скорости света.

4. Длина тел в разных системах.

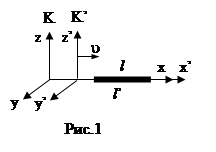Предположим, что некоторый стержень, находящийся в неподвижной системе К, расположен вдоль оси x и имеет в этой системе длину l.

Какова длина этого стержня в системе К’, движущейся относительно стержня со скоростью u в направлении оси x?

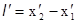
Координаты 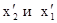надо измерять в один и тот же момент времени, определяемый в системе К’. Для этого выразим x через x’.

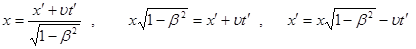
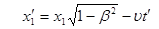
(4)

Стержень в координатной системе, движущейся относительно его, короче, чем в системе, где стержень покоится ().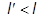

5. Релятивистский закон сложения скоростей.

В классической механике закон сложения скоростей, получающийся из преобразований Галилея, записывается так:

u – абсолютная скорость (скорость относительно неподвижной системы отсчета К), u’ – относительная скорость (скорость в движущейся системе отсчета К’), u – переносная скорость (скорость движения системы К’ относительно системы К).

Из преобразований Лоренца следует иная связь между перечисленными скоростями. Для установления этой связи запишем преобразования Лоренца для координаты и времени при переходе от системы К’ к системе К.

(5)

Возьмем дифференциал от формул (5):

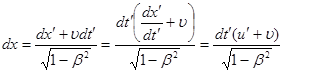(6)

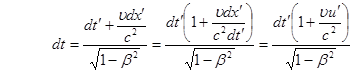(7)

Поделив (6) на (7) и учитывая, что 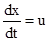, получим формулу для закона сложения скоростей в теории относительности:

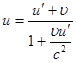(8)

При u<<c эта формула переходит в формулу классического закона сложения скоростей.

Рассмотрим некоторые частные случаи.

1. Пусть относительная скорость тела u’=c. Тогда из формулы (8) получим:

То есть получается, что и абсолютная скорость u=c.

2. Пусть относительная скорость тела u’=c и переносная скорость u=c. Тогда из формулы (8) получим:

То есть и в этом случае абсолютная скорость u=c.

Из этих примеров виден предельный характер скорости света, а также то, что скорость света одинакова во всех системах отсчета. Таким образом, постоянство скорости света непосредственно вытекает из преобразований Лоренца,

Дата добавления: 2015-05-10