Общая методика построения регрессионного уравнения

Теорема, обратная теореме Виета

Теорема Виета

Разложение квадратного трехчлена на множители

Особые случаи

Неполное квадратное уравнение:

Решать неполное квадратное уравнение можно способом, описанным выше, но можно использовать простые методы решения

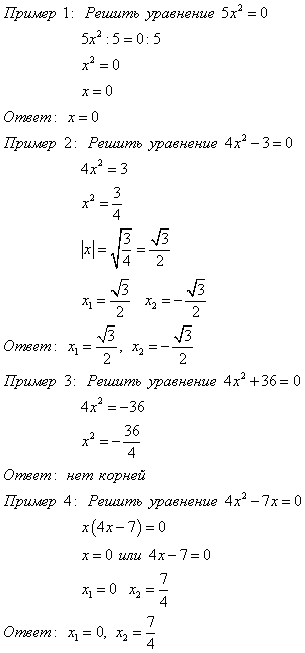
Квадратный трехчлен 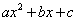с дискриминантом 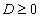можно разложить на множителе по формуле

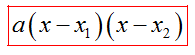
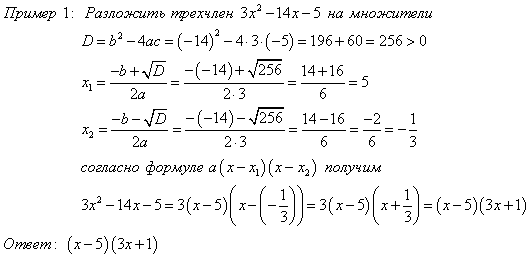
Приведенное квадратное уравнение имеет вид

т.е. коэффициент a=1.

Если x₁ и x₂ - корни приведенного квадратного уравнения, то

Если p, q, x₁, x₂ таковы, что

то x₁, x₂ - корни уравнения

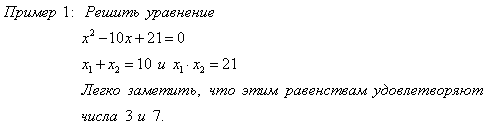
1) Выбираем зависимую переменную Y.

2) Рассматриваем парные графики зависимостей Y от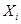

3) Анализируются исходные данные (описательные статистики, распределение, «выбросы» в данных)

По виду этого графика делаются выводы о наличии или отсутствии зависимости и о виде этой зависимости.

4) Рассматривается матрица корреляции между зависимой переменной и независимыми. Интерпретируются знаки линейной корреляции и сила линейной связи.

5) Рассматривается матрица корреляции между независимыми переменными. Если , то один из них исключается и/или преобразуются данные и/или строится ридж-регрессия.

6) С помощью метода пошагового отбора оценивается регрессия

7) Подбирается спецификация модели, максимизируя , минимизируется количество параметров линейной регрессии (ТЕСТЫ!!).

Подбирая спецификацию модели можно использовать следующие соображения:

· lnY, тогда зависимая переменная не уйдет в минус и зависимость Y от X постепенно.

· берется параметр в квадрате, если с увеличением X его влияние на Y возрастает.

· ln параметра. В этом случае с ростом значения параметра, влияние на Y уменьшается.

· использование взаимодействия параметров, например их перемножение.

8) Тестируются остатки подобранной модели (тест на нормальность, автокорреляция, гетероскедастичность!!)

9) Интерпретация полученных результатов:

· описание экономического смысла модели

· интерпретация коэффициентов и знаков перед ними

· анализ точности прогнозирования и ширины интервала (тест на точность прогнозов)

10) Построение интервального прогноза по наилучшей подобранной модели

Дата добавления: 2015-05-10