Розв'язок

Позначимо матрицю і вектори

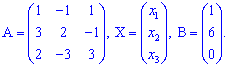
Матричний розв'язок системи алгебраїчних рівнянь шукаємо за формулою

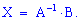
Для знаходження оберненої матриці 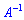обчислимо визначник

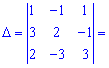
Оскільки 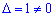, то задана система рівнянь сумісна і має єдиний розв'язок.

Знайдемо транспоновану матрицю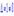

Знайдемо алгебраїчні доповнення до елементів заданої матриці:

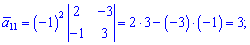
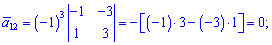
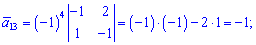
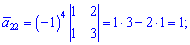
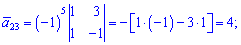
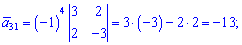
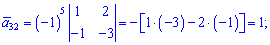
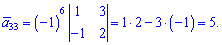
Обернену матрицю обчислюємо за формулою

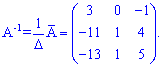
Знайдемо розв'язок СЛАР

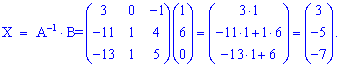
Розв'язок СЛАР:

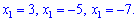
Метод Крамера (Крамера правило) — спосіб розв'язання квадратних систем лінійних алгебраїчних рівнянь із ненульовим визначником основної матриці (при цьому для таких рівнянь розв'язок існує і є єдиним). Метод було створено Габріелем Крамером у 1750 році.

Опис методу[ред. • ред. код]

Для системи 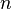лінійних рівнянь з 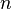невідомими (над довільним полем)

з визначником матриці системи , що не рівний нулю, розв'язок записується у такому вигляді:

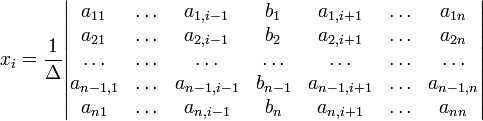
(i-й стовпчик матриці системи замінюється стовпчиком вільних членів).

Іншим чином правило Крамера формулюється так: для будь-яких коефіцієнтів c₁, c₂, …, c_n виконується рівність:

У такій формі формула Крамера справедлива без припущення, що не рівне нулю, не треба навіть, аби коефіцієнти системи були елементами цілісного кільця (визначник системи навіть може бути дільником нуля у кільці коефіцієнтів). Також можна вважати, що або набори 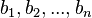та 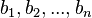, або набір 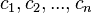складаються не з елементів кільця коефіциєнтів системи, а деякого модуля над цим кільцем. В такому вигляді формула Крамера використовується, наприклад, при доведенні формули для визначника Грама і Леми Накаями.

Приклад[ред. • ред. код]

Система лінійних рівнянь:

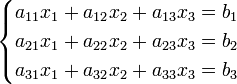
Визначники:

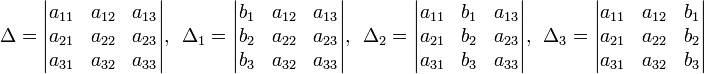
Розв'язок:

Приклад:

Визначники:

Дата добавления: 2015-05-10