
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Уравнение Пенга-Робинсона через коэффициент сверхсжимаемости
|
|
|
|
Математическая постановка задачи
Целью работы является получение мольных долей жидкой и газообразной фаз в трехкомпонентной смеси для каждой компоненты в отдельности. Задача сводится к нахождению и сравнению фугитивностей всех компонент.
Для решения поставленной задачи дается три компонента: дихлорбензол, метанол и изобутан, для которых и нужно решить задачу.
Таблица 1. Характеристики компонент смеси
| Название | Формула | 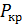 , атм , атм
| 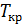 , К , К
|  , см3/моль , см3/моль
| 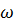
| Доля |
| Метанол | 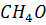
| 79,9 | 512,6 | 0,559 | 0,4 | |
| Изобутан | 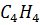
| 408,1 | 0,176 | 0,1 | ||
| Дихлорбензол | 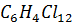
| 40,5 | 697,3 | 0,272 | 0,5 |
Чтобы вычислить условие равновесия (а это означает найти фугитивности для различных компонент и сравнить их) необходимо, как видно из формулы (11) знать коэффициент сверхсжимаемости.
Коэффициент сверх сжимаемости мы можем узнать из уравнения состояния (1), вводя новую переменную:

| (12) |
После подстановки (12) в (1) и приведя полученное уравнение к кубическому виду относительно  , получим:
, получим:

| (13) |
Это кубическое уравнение решается методом Кардано
Сперва делается замена

| (14) |
где  , это коэффициент при
, это коэффициент при 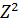 :
:

| (15) |
Таким образом, замена будет выглядеть следующим образом:

| (16) |
И после её подстановки в уравнение (13), уравнение примет вид:

| (17) |
где
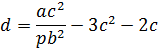
| (18) |

| (19) |
Корни этого уравнения находятся следующим образом: находим коэффициент 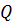

| (20) |
где, коэффициент при 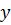

| (21) |
а  свободный член
свободный член

| (22) |
И при определенных значениях 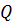 и
и  вычисляем корни нашего кубического уравнения:
вычисляем корни нашего кубического уравнения:
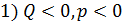
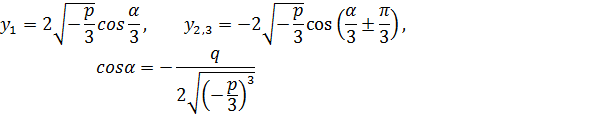

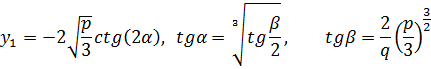
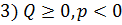
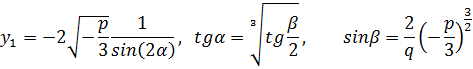
| (23) |
Задача, была бы простой, если бы наша система была однофазной, но поскольку она двухфазная, то нам необходимо вычислить молярные доли -того вещества в жидкой (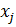 ) и газовой (
) и газовой (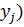 фазах. Эти данные нам необоходимы, чтобы найти константы
фазах. Эти данные нам необоходимы, чтобы найти константы 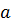 и
и  уравнения Пенга-Робинсона.
уравнения Пенга-Робинсона.
Для нахождения этих величин воспользуемся формулами:
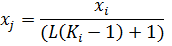
| (23) |
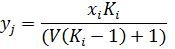
| (24) |
Где 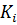 – коэффициент распределения -того вещества,
– коэффициент распределения -того вещества, 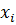 – мольная доля
– мольная доля  -того вещества.
-того вещества.
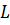 и
и 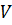 – константы, соответственно равные 0.000003 и 0.999997
– константы, соответственно равные 0.000003 и 0.999997
Коэффициент распределения находится по формуле:

| (25) |
Где  – давление в пласте, в нашем случае
– давление в пласте, в нашем случае 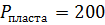 атмосфер.
атмосфер.
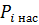 – давление насыщения -того вещества, которое находится по формуле
– давление насыщения -того вещества, которое находится по формуле

| (26) |
Где значения 
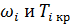 берутся из таблицы 1 для -того вещества соответственно.
берутся из таблицы 1 для -того вещества соответственно.
Коэффициент распределения мы так же можем найти и через отношение фугитивностей:
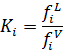
| (27) |
Где  – фугитивность -той компоненты в жидкой фазе,
– фугитивность -той компоненты в жидкой фазе,  – фугитивность
– фугитивность  -той компоненты в газовой фазе (фугитивность можем найти по формуле (11).
-той компоненты в газовой фазе (фугитивность можем найти по формуле (11).
Блок-схема программы
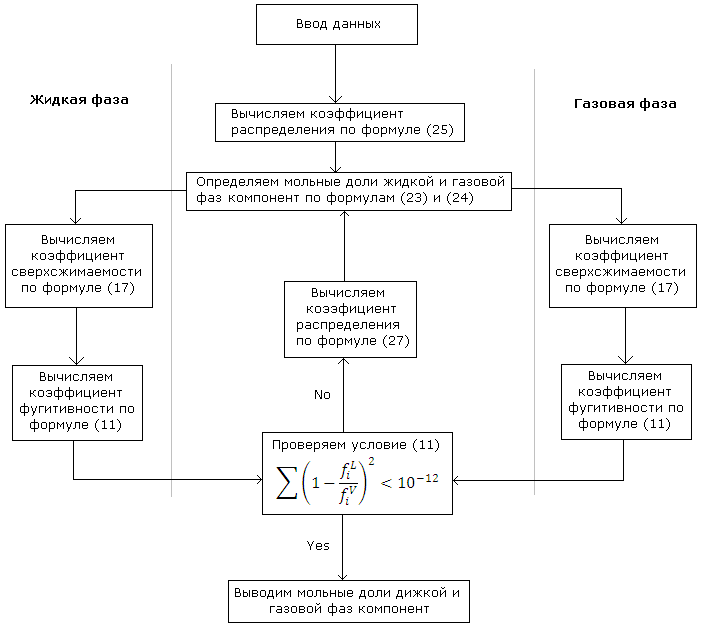
Рисунок 1. Блок-схема программы
|
|
|
|
|
Дата добавления: 2015-05-10; Просмотров: 2853; Нарушение авторских прав?; Мы поможем в написании вашей работы!