Достоинства и недостатки реляционной модели данных

Реляционная модель. Достоинства и недостатки

Достоинства реляционной модели:

-простота и доступность для понимания пользователем. Единственной используемой информационной конструкцией является "таблица";

-строгие правила проектирования, базирующиеся на математическом аппарате;

-полная независимость данных. Изменения в прикладной программе при изменении реляционной БД минимальны;

-для организации запросов и написания прикладного ПО нет необходимости знать конкретную организацию БД во внешней памяти.

Недостатки реляционной модели:

-далеко не всегда предметная область может быть представлена в виде "таблиц";

-в результате логического проектирования появляется множество "таблиц". Это приводит к трудности понимания структуры данных;

-БД занимает относительно много внешней памяти;

-относительно низкая скорость доступа к данным.

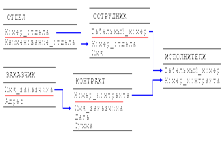
8.) Схема отношения

- это именованное множество пар {имя атрибута, имя домена (или типа, если понятие домена не поддерживается)}. Степень или "арность" схемы отношения - мощность этого множества. Степень отношения СОТРУДНИКИ равна четырем, то есть оно является 4-арным. Если все атрибуты одного отношения определены на разных доменах, осмысленно использовать для именования атрибутов имена соответствующих доменов (не забывая, конечно, о том, что это является всего лишь удобным способом именования и не устраняет различия между понятиями домена и атрибута).

9.)Реляционная алгебра

как теоретический язык запросов по сравнению с реляционным исчислением более наглядно описывает выполняемые над отношениями действия.

Примером языка запросов, основанного на реляционной алгебре, явля­ется ISBL (Information System Base Language — базовый язык информационных систем). Языки запросов, построенные на основе реляционной алгебры, в современных СУБД широкого распространения не получили. Однако знакомство с ней полезно для понимания сути реляционных операций, выражаемых другими используемыми языками.

Вариант реляционной алгебры, предложенный Коддом, включает в себя следующие основные операции: объединение, разность (вычитание), пересечение, декартово (прямое) произведение (или произведение), выборка (селекция, ограничение), проекция, деление и соединение.

Объединением двух совместимых отношений R1 и R2 одинаковой раз­мерности (Rl UNION R2) является отношение R, содержащее все элементы исходных отношений (с исключением повторений).

Вычитание (разность) совместимых отношений R1 и R2 одинаковой размерности (Rl MINUS R2) есть отношение, тело которого состоит из множества кортежей, принадлежащих R1, но не принадлежащих отношениюR2.

Пересечение двух совместимых отношений R1 и R2 одинаковой размер­ности (Rl INTERSECT R2) порождает отношение R с телом, включающим в себя кортежи, одновременно принадлежащие обоим исходным отноше­ниям. Рис.3.

Произведение отношения R1 степени к1 и отношения R2 степени к2 (Rl TIMES R2), которые не имеют одинаковых имен атрибутов, есть такое отношение R степени (к1+к2), заголовок которого представляет сцепление заголовков отношений R1 и R2, а тело — имеет кортежи, такие, что первые к1 элементов кортежей принадлежат множеству R1, а последние к2 элемен­тов — множеству R2. При необходимости получить произведение двух от­ношений, имеющих одинаковые имена одного или нескольких атрибутов, применяется операция переименования RENAME, рассматриваемая далее.

10.) Выборка (R WHERE f)

отношения R по формуле f представляет собой новое отношение с таким же заголовком и телом, состоящим из таких корте­жей отношения R, которые удовлетворяют истинности логического выраже­ния, заданного формулой f. Для записи формулы используются операнды — имена атрибутов (или номера столбцов), константы, логические операции (AND — И, OR — ИЛИ, NOT — НЕ), операции сравнения и скобки. Рис.5

Проекция отношения А на атрибуты X, Y,..., Z (А [X, Y,..., Z]), где множество {X, Y,..., Z} является подмножеством полного списка атрибутов заголовка отно­шения А, представляет собой отношение с заголовком X, Y,..., Z и телом, содер­жащим кортежи отношения А, за исключением повторяющихся кортежей. Повторение одинаковых атрибутов в списке X, Y,..., Z запрещается.

Операция проекции допускает следующие дополнительные варианты записи:

- отсутствие списка атрибутов подразумевает указание всех атрибутов (операция тождественной проекции);

- выражение вида R[ ] означает пустую проекцию, результатом которой является пустое множество;

- операция проекции может применяться к произвольному отношению, в том числе и к результату выборки.

Результатом деления отношения R1 с атрибутами А и В на отношение R2 с атрибутом В (Rl DIVIDEBY R2), где А и В простые или составные атрибу­ты, причем атрибут В — общий атрибут, определенный на одном и том же домене (множестве доменов составного атрибута), является отношение R с заголовком А и телом, состоящим из кортежей г таких, что в отношении R1 имеются кортежи (г, s), причем множество значений sвключает множество значений атрибута В отношения R2.

Соединение C_f(Rl, R2) отношений R1 и R2 по условию, заданному фор­мулой f, представляет собой отношение R, которое можно получить путем Декартова произведения отношений R1 и R2 с последующим применением к результату операции выборки по формуле f. Правила записи формулы f такие же, как и для операции селекции.

Другими словами, соединением отношения R1 по атрибуту А с отноше­нием R2 по атрибуту В (отношения не имеют общих имен атрибутов) явля­ется результат выполнения операции вида:

(Rl TIMES R2) WHERE A 0 В,

где Q — логическое выражение над атрибутами, определенными на од­ном (нескольких — для составного атрибута) домене. Соединение C_f(Rl, R2), где формула f имеет произвольный вид (в отличие от частных случаев, рассматриваемых далее), называют также Q-соединением.

Важными с практической точки зрения частными случаями соединения являются эквисоединение и естественное соединение.

Дата добавления: 2015-05-10