П. 3.1. Определение производной. Геометрически, механический, экономический смысл производной

Тема 3. Производная.

Задачи, приводящие к понятию производной.

1. Задача о скорости движущейся точки

Пусть s = s (t) представляет з акон прямолинейного движения материальной точки.

Это уравнение выражает путь s, пройденный точкой, как функцию времени t.

Обозначим через Δ s путь, пройденный за промежуток времени Δ t от момента t до t + Δ t, т. е.
Δ s = s (t + Δ t) - s (t). Отношение называется средней скоростью точки за время от t до t + Δ t.

Чем меньше Δ t, т. е. чем короче промежуток времени от t до t + Δ t, тем лучше средняя скорость характеризует движение точки в момент времени t. Поэтому естественно ввести понятие скорости v в данный момент t, определив ее как предел средней скорости за промежуток от t до t + Δ t, когда Δ t→ 0:

Величина v называется мгновенной скоростью точки в данный момент t.

2. Задача о касательной к данной кривой.

Пусть на плоскости хОу дана кривая уравнением у = f (х). Требуется провести касательную к данной кривой в данной точке M₀(x₀;f(x₀)) (Уравнение прямой проходящей через заданную точку с координатами (x₀,y₀) в заданном направлении y-y₀=k(x-x₀)).

Так как точка касания M₀ дана, то для решения задачи потребуется найти только угловой коэффициент искомой касательной, т. е. tg φ — тангенс угла наклона касательной к положительному направлению оси Ох (рис.1).
Рис.1

Для нахождения коэффициента касательной через точки M₀(x₀;f(x₀)) и M₁(x₀+∆x;f(x₀+∆x)) проведем секущую M₀M₁.

Из рис. видно, что угловой коэффициент tg α секущей M₀M₁ равен отношению 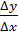, где ∆y= f(x₀+∆x)- f(x₀). Т.о. угловой коэффициент касательной M₀T к данной кривой в точке M₀ можно найти на основании следующего определения:

Определение. К асательной к кривой в точке M₀ называется прямая M₀T, угловой коэффициент которой, равен пределу углового коэффициента секущей M₀M₁, когда . Отсюда следует, что

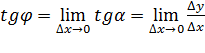
Определение. Производной функции 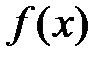называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует):

.

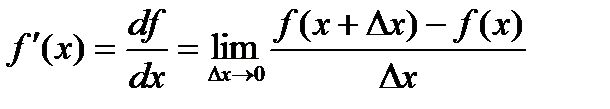Значение производной функции в какой-либо данной точке 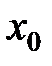обозначается обычно или .

Геометрический смысл производной. Значение производной равно угловому коэффициенту касательной к графику функции 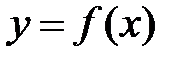в точке с абсциссой :

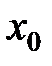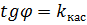= . (Уравнение касательной y- f(x₀)= (x-x₀))

Механический смысл производной. Пусть задан путь s = s (t) движения материальной точки. Скорость данной материальной точки в момент времени t есть производная от пути s по времени t: v(t)=

Определение. Пусть функция 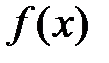имеет конечную производную в точке x, тогда функция называется дифференцируемой в этой точке. Функция, дифференцируемая во всех точках промежутка Х, называется дифференцируемой на этом промежутке.

п. 3.2. Схема вычисления производной. Основные правила дифференцирования.

Схема вычисления производной функции y=f(x):

1. Дадим аргументу x приращение 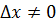и найдем наращенное значение функции y+∆y= f(x+∆x).

2. Находим приращение функции ∆y= f(x+∆x)- f(x)

3. Составляем отношение .

4. Находим предел этого отношения при 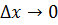, т.е. 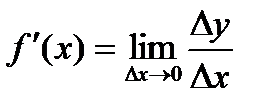(если этот предел существует).

Если функции u(x) и v(x) дифференцируемые, то справедливы следующие правила дифференцирования:

1. (u+v)¢=u¢+v¢

2. (u-v)¢=u¢-v¢

3. (uv)¢=u¢v+uv¢

4. (cu)¢=cu¢

5.

п. 3.3. Производная сложной функции.

Теорема. Если функции и дифференцируемы от своих аргументов, то существует производная сложной функции 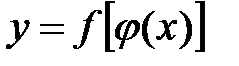и равна производной данной функции по промежуточному аргументу, умноженной на производную самого промежуточного аргумента по независимой переменной x, т.е.

.

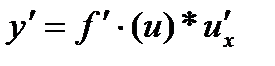Пример. Найти производную функции .

Решение.

.

п. 3.4. Производные основных элементарных функций.

(c) ¢ =0; (x) ¢ =1

простые	сложные
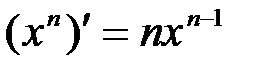
степенная	степенная (u^n)¢=nu^n-1u¢
показательная (e^x)¢= e^x (a^x)¢=a^xlna	показательная (e^u)¢= e^uu¢ (a^u)¢=a^ulna*u¢
логарифмическая (ln x)¢= 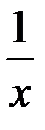(logax)¢=	логарифмическая (ln u)¢= 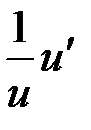(logau)¢=
тригонометричекая (sin x)¢=cos x (cos x)¢=-sin x (tg x)¢= 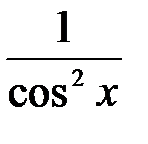(ctg x)¢=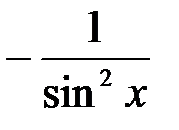	тригонометричекая (sin u)¢=cos u*u¢ (cos u)¢=-sin u*u¢ (tg u)¢= 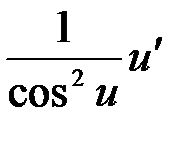(ctg u)¢=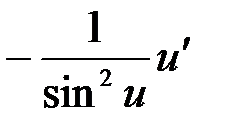

Производная степенно-показательной функции

Определение. Функция вида

, ,

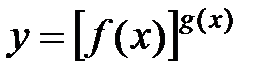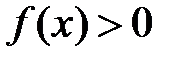где и основание, и показатель изменяются вместе с независимой переменной, называется степенно-показательной.

Найдем ее производную .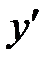

1) Прологарифмируем данную функцию:

.

2) Продифференцируем полученное тождество. С одной стороны:

.

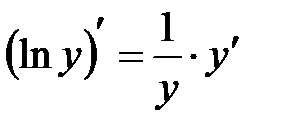С другой стороны:

.

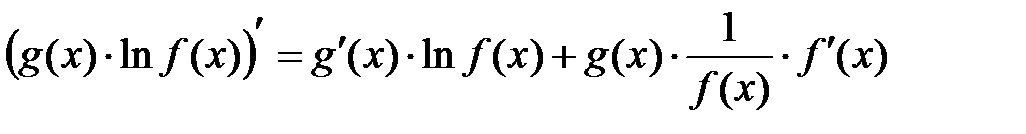Следовательно:

.

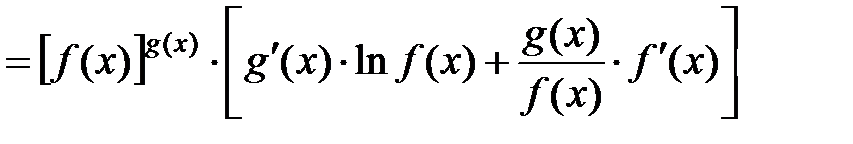Определение. Операция, состоящая в последовательном применении к функции 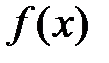сначала логарифмирования (по основанию ), а затем дифференцирования, называется логарифмическим дифференцированием, а ее результат

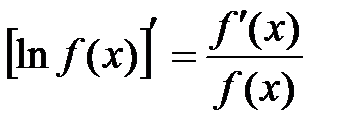
– логарифмической производной от функции .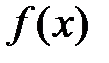

Пример. 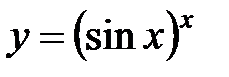. Найти .

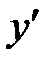Решение.

1) .

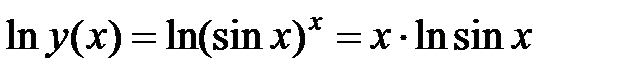2) С одной стороны: ;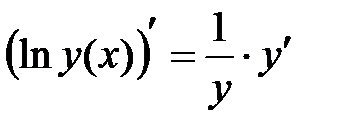

С другой стороны: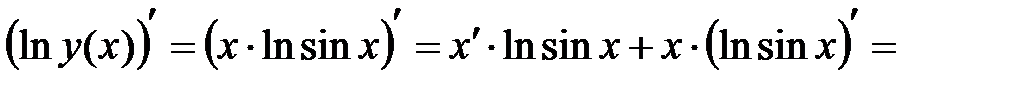

.

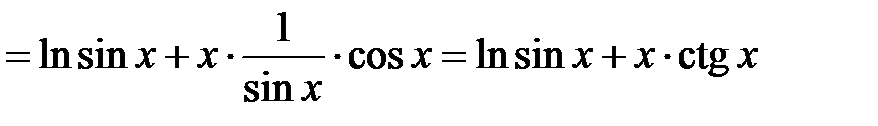Следовательно, .

Производные высших порядков

Определение. Допустим, что функция 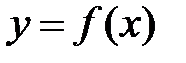имеет производную в некотором интервале независимой переменной . Производная от 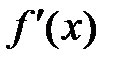(если она существует) называется производной второго порядка или второй производной от первоначальной функции 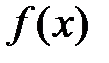и обозначается :

.

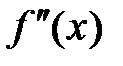Определение. Таким же образом производной третьего порядка или третьей производной 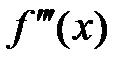от функции 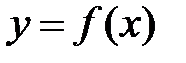называется производная от производной второго порядка.

Определение. Производной 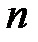- го порядка называется производная от производной 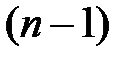-го порядка

.

Все свойства, которые имеют место для первой производной функции, сохраняются и для второй производной и для производной 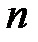-го порядка.

Пример.

, , , …,

.

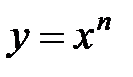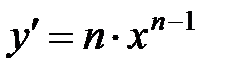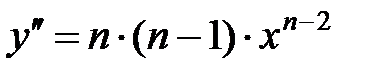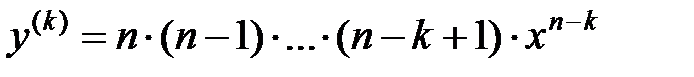Дата добавления: 2015-05-10