Схемы выбора без повторений

Контрольные вопросы

1. Сформулируйте комбинаторный принцип сложения.

2. Сформулируйте комбинаторный принцип умножения.

3. Что называют размещением без повторений? По какой формуле вычисляют число размещений без повторений из n элементов по m элементов?

4. Что называют перестановкой без повторений? По какой формуле вычисляют число перестановок без повторений?

5. Что называют сочетанием без повторений? По какой формуле вычисляют число сочетаний без повторений из n элементов по m элементов?

Упражнения

1. На книжной полке стоят 20 книг по алгебре, 12 – по теории вероятностей, 7 – по математическому анализу и 25 по литературе. Сколькими способами можно выбрать одну книгу по математике?

2. Сколько трехзначных чисел можно составить из цифр 1, 3, 5, если цифры в числе не повторяются?

3. Имеется 5 билетов денежно-вещевой лотереи, 6 билетов спортлото и 10 билетов автомотолотереи. Сколькими способами можно выбрать один билет спортлото или автомотолотереи?

4. Сколько различных полных обедов можно составить, если в меню имеется 3 первых, 2 вторых и 2 третьих блюда?

5. В отряде 5 разведчиков, 4 связиста и 2 санитара. Сколькими способами можно выбрать одного солдата так, чтобы он был разведчиком или санитаром? Сколькими способами можно составить разведгруппу из трех человек, чтобы в нее вошли разведчик, связист и санитар?

6. Сколько можно получить различных четырехзначных чисел, вставляя пропущенные цифры в число

а. *2*5;

б. 3*7*.

7. Сколькими способами можно выбрать один цветок из корзины, в которой имеется 12 гвоздик, 15 роз и 7 хризантем?

8. У одного школьника имеется 7 различных книг для обмена, а у другого – 16. Сколькими способами они могут осуществить обмен: а) книга на книгу; б) две книги на две книги?

9. Сколькими способами можно выбрать 5 карт из колоды, в которой 36 карт?

10. Из группы в 25 человек нужно выделить 3 человека на дежурство. Сколькими различными способами это можно сделать?

11. На собрании членов кооператива присутствуют 20 человек. Сколькими способами можно выбрать:

а. правление кооператива в составе 5 человек;

б. председателя правления, его заместителя и бухгалтера.

12. Из 4 первокурсников, 5 второкурсников и 6 третьекурсников надо выбрать 3 студентов на конференцию. Сколькими способами можно осуществить этот выбор, если среди выбранных должны быть студенты разных курсов?

13. В шахматном кружке 12 юношей и 8 девушек. Для участия в соревнованиях из них нужно составить команду, в которую должны войти 9 юношей и 3 девушки. Сколькими способами это можно сделать?

14. Сколькими способами три награды могут быть распределены между 10 участниками соревнования?

15. Группа студентов изучает десять различных дисциплин. Сколькими способами можно составить расписание занятий на понедельник, если в это день должно быть 4 разных занятия?

16. На 9-ти карточках написано по одной цифре от 1 до 9 без повторений. Располагая любые 3 карточки в строку, мы получим трехзначное число. Сколько различных трехзначных чисел можно изобразить при помощи этих 9-ти карточек?

17. Сколькими способами можно сформировать программу конференции, выбрав из 20 участников четырех, выступающих с докладами?

18. Сколько различных слов, состоящих из трех букв, можно составить из букв слова БУРАН?

19. В электричке 12 вагонов. Сколько существует способов размещения 4 пассажиров, если в одном вагоне должно быть не более одного пассажира?

20. Имеется 15 различных книг и книжная полка, вмещающая 12 книг. Сколько существует способов заполнить полку имеющимися книгами?

21. Из 10 мальчиков и 10 девочек спортивного класса для участия в эстафете надо составить три команды, каждая из которых состоит из одного мальчика и одной девочки?

22. Сколькими способами можно расположить шесть различных книг в ряд на одной полке?

23. Сколькими способами 5 человек могут встать в очередь друг за другом?

24. Алхимик использует семь ингредиентов для приготовления эликсира жизни. Сколько существует различных порядков вливания их в сосуд?

25. Сколькими способами можно расставить на полке 7 различных книг, чтобы определенные три книги стояли рядом? Не рядом?

26. Сколько шестизначных чисел, кратных пяти, можно составить из цифр 1, 2, 3, 4, 5, 6 при условии, что в числе цифры не повторяются?

27. Сколькими способами можно рассадить 5 человек за круглым столом? (Рассматривается только расположение сидящих относительно друг друга).

Схемы выбора с повторениями

Контрольные вопросы

1. Что называют размещением с повторениями? По какой формуле вычисляют число размещений с повторениями из n элементов по m элементов?

2. Что называют перестановкой с повторениями? По какой формуле вычисляют число перестановок с повторениями?

3. Что называют сочетанием с повтореними? По какой формуле вычисляют число сочетаний с повтореними из n элементов по m элементов?

Упражнения

28. Сколькими способами можно составить набор из 6 пирожных, если имеется 4 сорта пирожных?

29. На почте имеются марки 10 различных типов. Сколько существует способов купить 15 марок?

30. В цветочном магазине продаются цветы шести сортов. Сколько можно составить различных букетов из девяти цветов в каждом? (Букеты, отличающиеся только расположением цветов, считаются одинаковыми.)

31. Имеются пирожные 7 различных типов. Пирожные одного и того же типа считаем неразличимыми. Сколько существует различных способов покупки 12 пирожных?

32. В почтовом отделении продаются открытки десяти видов. Сколькими способами можно купить здесь набор из 8 открыток, если открыток каждого вида имеется не менее 8 штук?

33. Сколькими способами можно распределить 12 различных учебников между 4 студентами?

34. Известно, что 7 студентов сдали экзамен по теории вероятности на хорошо и отлично. Сколькими способами могли быть поставлены им оценки?

35. Сколькими способами можно распределить 6 различных подарков между 4 ребятами?

36. Сколько различных инициалов (ФИО) можно образовать, используя 5 первых букв русского алфавита?

37. Сколькими способами можно разложить в два кармана 9 монет разного достоинства?

38. Сколько существует различных шестибуквенных слов, которые можно составить из слова «АНАНАС»?

39. Сколько «слов» можно получить, переставляя буквы в слове: а) «ГОРА»; б) «ИНСТИТУТ»?

40. Сколько «слов» можно получить, переставляя буквы в слове: а) «МОРЕ»; б) «АБРАКАДАБРА»?

41. Сколько существует способов размещения 9 человек в двухместный, трехместный и четырехместный номера гостиницы?

42. Сколькими способами можно распределить 16 видов товаров по трем магазинам, если в 1-й магазин надо доставит 9, во 2-й – 4, а в 3-й – 3 вида товаров?

43. В урне 12 белых и 8 черных шаров. Сколькими способами можно выбрать 5 шаров, чтобы среди них было: а) 5 черных; б) 3 белых и 2 черных?

44. Из группы, состоящей из 7 мужчин и 4 женщин, нужно выбрать 6 человек так, чтобы среди них было не менее двух женщин.

45. Сколькими способами можно распределить 4 книги на трех полках книжного шкафа? Найти число способов расстановки книг на полке, если порядок их расположения имеет значение.

46. Сколько чисел, больших 100, можно записать с помощью цифр 0, 1, 3, 5, 6 (без повторений)?

47. Даны натуральные числа от 1 до 30. Сколькими способами можно выбрать три числа так, чтобы их сумма была четной.

Биномиальные коэффициенты. Треугольник Паскаля

Контрольные вопросы

1. Запишите формулу бинома Ньютона.

2. Что такое треугольник Паскаля?

3. Какими свойствами обладают биномиальные коэффициенты?

Упражнения

48. Вычислите:

а.	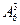б.	в.	г.
д.	е.	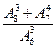ж.	з.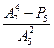

49. Разложите, используя бином Ньютона:

а. ;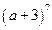

б. ;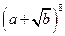

в.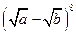

г. Разложите по формуле бинома Ньютона .

50. Найдите:

а. девятый член разложения ;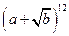

б. шестой член разложения ;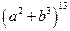

в. средний член разложения .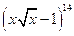

51. Найдите член разложения 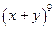, содержащий .

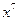52. Найдите член разложения , содержащий .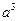

53. Найдите член разложения 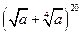, содержащий .

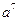54. Решите уравнения:

а. ;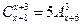

б. ;

в. ;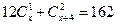

г. ;

д. ;

е. .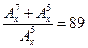

Дата добавления: 2015-05-10