Общее уравнение плоскости

Исследование общего уравнения плоскости

Общее уравнение плоскости

2. Уравнение плоскости “в отрезках”

О п р е д е л е н и е 1. Общим уравнением плоскости называется линейное уравнение первой степени относительно трех переменных: х, у и z, т.е. уравнение вида Ax + By + Cz + D = 0. (1) Коэффициенты при х, у и z являются координатами вектора, который перпендикулярен плоскости.

О п р е д е л е н и е 2. Всякий вектор, перпендикулярный плоскости, называется нормальным вектором этой плоскости.

Если известна фиксированная точка M ₀ (x ₀, y ₀, z ₀), лежащая в данной плоскости, и вектор , перпендикулярный данной плоскости, то уравнение плоскости, проходящей через точку M ₀ (x ₀, y ₀, z ₀), перпендикулярно вектору , имеет вид

A (x-x ₀) + B (y-y ₀) + C (z-z ₀)= 0. (2)

Покажем, что уравнение (2) является общим уравнением плоскости (1). Для этого раскроем скобки и соберем в скобки свободный член:

. Ax + By+ Cz + (-Ax ₀ - By -Cz ₀)= 0

Обозначив D = -Ax ₀ - By -Cz ₀, получим уравнение Ax + By + Cz + D = 0.

Задача 1. Составить уравнение плоскости, проходящей через точку А, перпендикулярно вектору , если A (4, -3, 1), B (1, 2, 3).

Решение. Найдем нормальный вектор плоскости :

.

Для нахождения уравнения плоскости используем уравнение (2):

Ответ: -3 x + 5 y + 2 z + 25 = 0.

Задача 2. Составить уравнение плоскости, проходящей через точку M ₀ (-1, 2, -1), перпендикулярно оси OZ.

Решение. В качестве нормального вектора искомой плоскости можно взять любой вектор, лежащий на оси OZ, например, 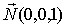, тогда уравнение плоскости

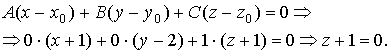
Ответ: z + 1 = 0.

2. Уравнение плоскости “в отрезках”

Рассмотрим общее уравнение плоскости Ax + By + Cz + D = 0. Перенесем свободный член в правую часть уравнения и разделим обе части уравнения на (– D).

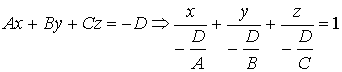
Обозначив , получим уравнение плоскости “в отрезках”

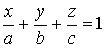, (3)

где a, b, c – это отрезки, которые отсекает плоскость от координатных осей.

Задача 1. Найти точки пересечения плоскости 2 x - 3 y - 4 z -24 = 0 с осями координат.

Решение. Приведем уравнение плоскости к уравнению “в отрезках”:

Тогда координаты точек M 1 (12, 0, 0), M 2 (0, -8, 0), M 3 (0, 0, -6). Ответ: M 1 (12, 0, 0), M 2 (0, -8, 0), M 3 (0, 0, -6).

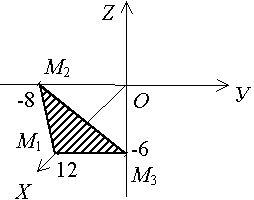
Задача 2. Плоскость проходит через точку M ₁ (6, -10, 1) и отсекает на оси абсцисс отрезок а = -3 и на оси аппликат - отрезок с = 2. Составить для этой плоскости уравнение “в отрезках”.

Решение. Уравнение “в отрезках” . Найдем значение отрезка b. Для этого подставим в данное уравнение координаты точки M ₁.

.

Ответ: .

Задача 3. Составить уравнение плоскости, отсекающей на оси OZ отрезок с = -5, перпендикулярно к вектору .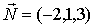

Решение. Будем использовать общее уравнение плоскости

.

Приведем полученное уравнение к уравнению “в отрезках”:

;

,

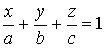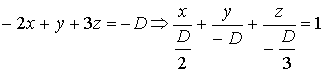где 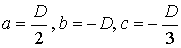, но 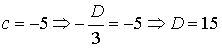. Тогда и b = -15, и уравнение плоскости имеет вид

.

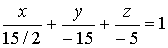Приведем это уравнение к общему уравнению плоскости

.

Ответ: 2 x - y - 3 z - 15 = 0.

Дата добавления: 2015-05-10