
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Принцип двоїстості. Теорема Дезарга
|
|
|
|
Правила дифференцирования
Вопрос 37
Ч 2 ст 75
Отличия:
1.Общие основания рег-ся нормаи общ части, а спец – в примечаниях к статьям особ части
2. Лицо совершившее прест иной категории
Спец основания освоб от УО:
- примечания которые направлены на снижение латентности отдельных видов преступления. Пример: ст 291, ст 291.1 дача взятки и посреднич-во во взятке.
- минимизация общественно-опасных последствий - ст 126
- реализация конституционных положений, например ст 308 – отказ свидетеля и потерпевшего от дачи показаний, ст 316 – укрывательство
- сложная жизненная ситуация, ст 151
- опред компромисс в борьбе с преступностью, ст 222, 223, 228
Есть уже апрельская редакция УК РФ.
1)  ,
,
2) 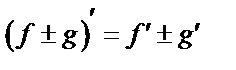 ,
,
3) 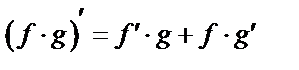 ,
,
4) 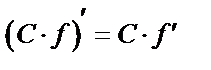 ,
,
5)  .
.
Таблица производных основных элементарных ф-й.
1.  1a)
1a) 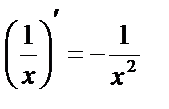
1б) 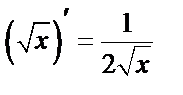
2. 
3. 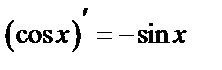
4. 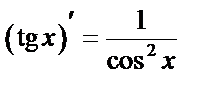
5. 
6. 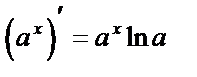
7. 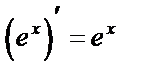
8. 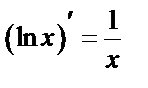
9. 
10. 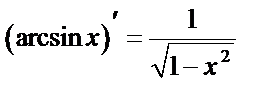
11. 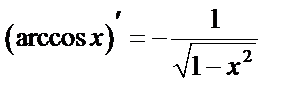
12. 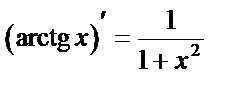
13. 
Таблица производных сложных ф-й 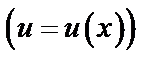
 или
или 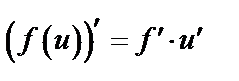
1. 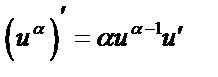
1a)  1б)
1б) 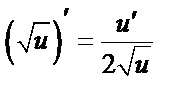
2. 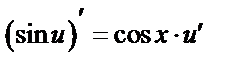
3. 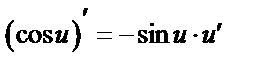
4. 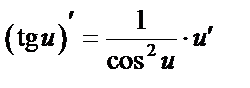
5. 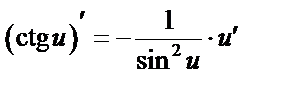
6. 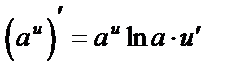
7. 
8. 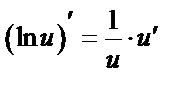
9. 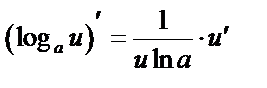
10. 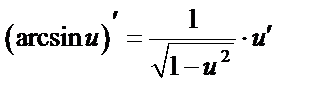
11. 
12. 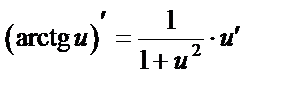
13. 
Нехай задано проективну площину Р2, яка породжена 3-ох вимірним векторним просторм V3. Тепер R лежить на площині Р2, R належить Р2.
Позначимо Р* множину всіх прямих площини Р2. Нехай відображення f площину Р2 переводить у Р*, тоді будь яку точку М з Р2 відображення переведе у пряму з Р*, таку, що координати точки М переведе у координати прямої М→m є Р*I М(m1, m2, m3)R, m: x1m1+x2m2+x3m3=0.
1. Перевіримо чи відображення f інєктивне. Візьмемо довільні 2 точки M i Nє Р2, тоді f(М)=m: m1 x1+m2 x2+m3 x3=0 є Р*, f(N)=n: n1 x1+n2 x2+n3 x3=0 є Р*. Якщо точки M i N не співпадають, то координати не рівні, тоді m≠n
2. f-сюрєктивне. Візьмемо пряму m є Р*, m: m1 x1+m2 x2+m3 x3=0 тоді існує довільна точка М(m1, m2, m3) і точка М є прообразом прямої m. Звідси випливає, що f -бієктивне. f -1: Р*→ Р2-бієктивне. При f, f -1 зберігається взаємна незалежність точок і прямих. Нехай точки А, B, C є d. Тоді відображеня f: А→а, В→b, C→c а при f -1 d→D. Точка А(а1,а2,а3)R має координати в репері R. d: d1 x1+d2 x2+d3 x3=0.
Якщо Ає d, то d1 а1+d2 а2+d3 а3=0. Звідси випливає, що D(d1, d2, d3)є а 

Тому якщо A,B,C є d, то a,b,c э D. Отже образом точок прямої при відображенні f є пучок прямих, а при відображені f -1- образом пучка є точки прямої.
Принцип двоїстості на площині: Якщо справедливе твердження у якому йде мова про точки, прямі та відношення належності між ними, то буде справедливе твердження яке одержується такою заміною слів:
Точка→пряма, пряма→точка, лежить на→проходить через.
Принцип двоїстості у просторі: Якщо справедливе твердження у якому йде мова про точки, прямі, площини та відношення між ними, то буде справедливе і таке твердження яке одержується такою заміною слів:
точка→площина, пряма→пряма, площина→точка, лежить на→проходить через, проходить через→лежить на.
Теорема Дезарга.
Означення: трьохвершинником називається фігура, яка складається з 3-ох точок, що не лежать на одній прямій і 3-ох прямих, які попарно з’єднують ці точки.

Теорема Дезарга: нехай задано 2-а 3-ох вершинними ∆АВС і ∆А1В1С1 відповідні елементи яких не співпадають, тоді
1. якщо АА1∩ВВ1∩СС1=S, то W є UV причому
U=AB∩ A1B1
V=BC∩B1C1
W=AC∩A1C1
2. якщо W є UV причому
U=AB∩ A1B1
V=BC∩B1C1
W=AC∩A1C1
То АА1∩ВВ1∩СС1=S.

1. Точки W, U, V лежать на першій прямій якщо визначник складений з їх координат =0. Які ж координати мають точки W, U, V?
Т. U=AB∩ A1B1, V=BC∩B1C1, W=AC∩A1C1
Щоб знайти координати A1B1, B1C1, A1C1, потрібно знати координати точок A1, B1, C1.
Розглянемо проективний репер R=(A,B,C,S)
A(1,0,0), B(0,1,0), C(0,0,1), S(1,1,1)
Знайдемо координати т. A1(a1,a2,a3) в репері R
A1 є SA звідси  =0
=0
a2= a3
A1(a1,a2,a3)R  A1(
A1( , 1,1)⇒ A1(α,1,1)R. Аналогічно В(1,ẞ,1), С(1,1, ᵞ)
, 1,1)⇒ A1(α,1,1)R. Аналогічно В(1,ẞ,1), С(1,1, ᵞ)
U= 
AB:  =0
=0
X3=0
A1B1: 
X1(1-ẞ)-X2( X3(
X3(
U=  ⇒
⇒  ⇒
⇒ 
U(
Аналогічно
V:  ⇒ V
⇒ V 
W:  ⇒W
⇒W 
 =
= 
Точки U,W,V лежать на одній прямій. Отже теорема справедлива за принципом двоїстості.
|
|
|
|
Дата добавления: 2015-05-10; Просмотров: 1095; Нарушение авторских прав?; Мы поможем в написании вашей работы!