Усеченное нормальное распределение

26)

Известно, что корректность использования классического нормального распределения наработки, достигается при Т₀ 3S.

При малых значениях Т₀ и большом ^ S, может возникать ситуация, когда ПРО f(t) «покрывает» своей левой ветвью область отрицательных наработок (рис. 4).

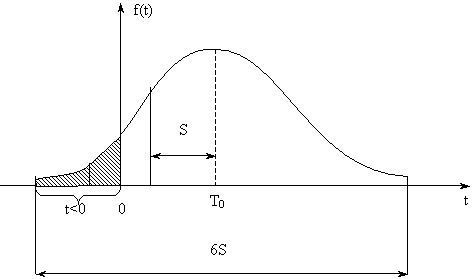
Рис. 4

Таким образом, нормальное распределение являясь общим случаем распределения случайной величины в диапазоне (- 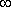; 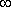), лишь в частности (при определенных условиях) может быть использовано для моделей надежности.

Усеченным нормальным распределением называется распределение, получаемое из классического нормального, при ограничении интервала возможных значений наработки до отказа.

В общем случае усечение может быть:

• 
  левым – (0; );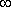
• 
  двусторонним – (t₁ , t₂).

Смысл усеченного нормального распределения (УНР) рассмотрен для случая ограничения случайной величины наработки интервалом (t₁ , t₂).

Плотность УНР 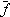(t) = c f(t),

где

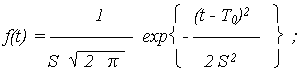
c – нормирующий множитель, определяемый из условия, что площадь под кривой 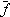(t) равна 1, т. е.

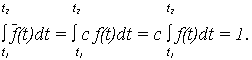
Откуда

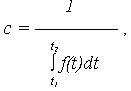
где

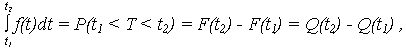
Применяя переход от случайной величины ^ Т = {t} к величине X = {x}:

x₂ = (t₂ – Т₀)/S; x₁ = (t₁ – Т₀)/S,

получается

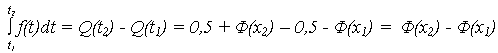
поэтому нормирующий множитель c равен:

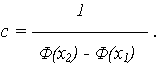
Поскольку [ 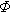(x) (x₂) - 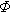(x) (x₁)] < 1, то c > 1, поэтому 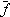(t) > f(t). Кривая 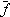(t) выше, чем f(t), т. к. площади под кривыми 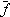(t) и f(t) одинаковы и равны 1 (рис. 5).

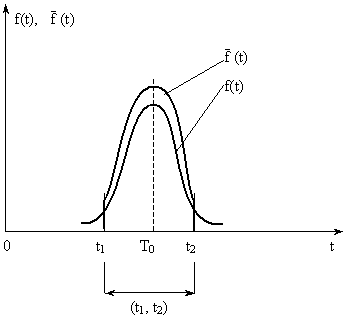
Рис. 5

Показатели безотказности для УНР в диапазоне (t₁ , t₂):

УНР для положительной наработки до отказа – диапазон (0; 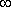) имеет ПРО

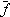(t) = c₀ f(t),

где c₀ – нормирующий множитель определяется из условия:

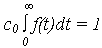
и равен (аналогично предыдущему):

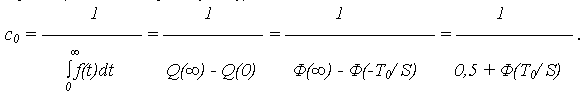
Показатели безотказности УНР (0; )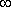

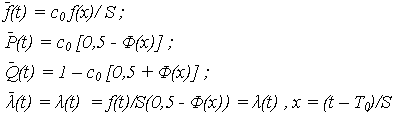
Изменение нормирующего множителя c₀ в зависимости от отношения Т₀ /S приведено на рис. 6.

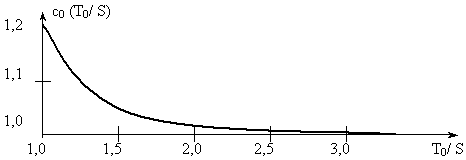
Рис. 6.

При Т₀ = S, Т₀ / S = 1 c₀ = max (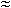 1,2).

При Т₀ / S 2,5 c₀ = 1,0, т.е. 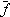(t)(t) = f(t).

Дата добавления: 2015-05-10