Тема: Ряды динамики

Вопросы:

1. Понятие и виды рядов динамики.

2. Сравнительная характеристика рядов динамики

3. Показатели рядов динамики

4. Средние показатели рядов динамики.

5. Изучение основной тенденции развития ряда динамики (тренда)

1. Понятие и виды рядов динамики.

Ряды динамики – статистические данные, отображающие развитие во времени изучаемого явления. Их также называют динамическими рядами, временными рядами.

В качестве показаний времени в рядах динамики выступают либо определенные даты (моменты), либо отдельные периоды (годы, кварталы, месяцы, сутки).

Уровни рядов динамики отображают количественную оценку (меру) развития во времени изучаемого явления. Они могут выражаться абсолютными, относительными или средними величинами.

Ряды динамики подразделяются на: моментные и интервальные.

Моментные ряды динамики отображают состояние изучаемых явлений на определенные даты (моменты) времени.

Списочная численность работников магазина в 2011 году

Дата	1.01.11	1.04.11	1.07.11	1.10.11
Число работников, чел.

Интервальные ряды динамики отражают итоги развития (функционирования) изучаемых явлений за отдельные периоды (интервалы) времени.

Объем розничного товарооборота магазина в 2005 - 2008 гг.

Год
Объем розничного товарооборота, тыс. р.	8850,7	9320,6	9800,1	10280,7

Классификация рядов динамики:

1. В зависимости от способа выражения уровней:

а) абсолютные

б) относительные

в) средние

2. В зависимости от того, как выражают уровни ряда состояние явления:

а) моментные

б) интервальные

3. В зависимости от расстояния между уровнями ряда динамики:

а) с равностоящими во времени уровнями

б) с неравностоящими во времени уровнями

5. Изучение основной тенденции развития ряда динамики (тренда)

Всякий ряд динамики теоретически может быть представлен в виде составляющих:
1) тренд – основная тенденция развития динамического ряда

(к увеличению либо снижению его уровней);
2) циклические (периодические) колебания, в том числе сезонные;
3) случайные колебания.

Изучение тренда включает два основных этапа:
1)ряд динамики проверяется на наличие тренда;

2) производится выравнивание временного ряда и непосредственное выделение тренда с экстраполяцией полученных результатов.

Наличие тренда можно определяется несколькими методами, например, используя критерий Стьюдента.

Для этого ряд распределения делится на две части (равные или почти равные), затем вычисляется экспериментальное значение критерия Стьюдента по формуле:

,

где

- выборочные средние (средние арифметические) двух частей временного ряда соответственно;

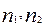- число уровней двух частей временного ряда соответственно;

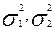- дисперсии двух частей временного ряда соответственно.

Затем полученное значение сравнивается с табличным

(α – уровень значимости; f – число степеней свободы, f = n-2).

Если табличное значение меньше экспериментального, тренд существует.

Непосредственное выделение тренда может быть произведено тремя методами:

1. Укрупнение интервалов. Ряд динамики разделяют на некоторое достаточно большое число равных интервалов. Если средние уровни по интервалам не позволяют увидеть тенденцию развития явления, переходят к расчету уровней за большие промежутки времени, увеличивая длину каждого интервала (одновременно уменьшается количество интервалов).

2. Скользящая средняя. В этом методе исходные уровни ряда заменяются средними величинами, которые получают из данного уровня и нескольких симметрично его окружающих. Целое число уровней, по которым рассчитывается средн ее значение, называют интервалом сглаживания. Интервал может быть нечетным (3, 5, 7 и т.д. точек) или четным (2, 4, 6 и т.д. точек).

При нечетном сглаживании полученное среднее арифметическое значение закрепляют за серединой расчетного интервала, при четном этого делать нельзя. Поэтому при обработке ряда четными интервалами их искусственно делают нечетными, для чего образуют ближайший больший нечетный интервал, но из крайних его уровней берут только 50 %.

Недостаток методики сглаживания скользящими средними состоит в условности определения сглаженных уровней для точек в начале и конце ряда. Получают их специальными приемами – расчетом средней арифметической взвешенной.

Так, при сглаживании по трем точкам выровненное значение в начале ряда рассчитывается по формуле:

Для последней точки расчет симметричен

При сглаживании по пяти точкам таких «дополнительных» формул будет четыре, по семи точкам – шесть и т.д.

3. Аналитическое выравнивание. Под этим понимают определение основной проявляющейся во времени тенденции развития изучаемого явления. Развитие предстает перед исследователем как бы в зависимости только от течения времени. В итоге выравнивания временного ряда получают наиболее общий, суммарный, проявляющийся во времени результат действия всех причинных факторов.

Отклонение конкретных уровней ряда от уровней, соответствующих общей тенденции, объясняют действием факторов, проявляющихся случайно или циклически. В результате приходят к трендовой модели

где f(t)– уровень, определяемый тенденцией развития;

e_t – случайное и циклическое отклонение от тенденции.

Целью аналитического выравнивания динамического ряда является определение аналитической или графической зависимости f(t). На практике по имеющемуся временному ряду задают вид и находят параметры функции f(t), а затем анализируют поведение отклонений от тенденции. Функцию f(t) выбирают таким образом, чтобы она давала содержательное объяснение изучаемого процесса.

Чаще всего при выравнивании используются следующие зависимости:

Линейная зависимость выбирается в тех случаях, когда в исходном временном ряду наблюдаются более или менее постоянные абсолютные цепные приросты, не проявляющие тенденции ни к увеличению, ни к снижению.

Параболическая зависимость используется, если абсолютные цепные приросты сами по себе обнаруживают некоторую тенденцию развития, но абсолютные цепные приросты абсолютных цепных приростов (разности второго порядка) никакой тенденции развития не проявляют.

Экспоненциальные зависимости применяются, если в исходном временном ряду наблюдается либо более или менее постоянный относительный рост (устойчивость цепных темпов роста, темпов прироста, коэффициентов роста), либо, при отсутствии такого постоянства, – устойчивость в изменении показателей относительного роста (цепных темпов роста цепных же темпов роста, цепных коэффициентов роста цепных же коэффициентов или темпов роста и т.п.).

Оценка параметров (a₀, a₁, a₂,...) осуществляется следующими методами:

1)методом избранных точек

2)методом наименьших расстояний

3) методом наименьших квадратов (МНК).

В большинстве расчетов используют метод наименьших квадратов, который обеспечивает наименьшую сумму квадратов отклонений фактических уровней от выравненных: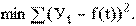

При линейной зависимости уравнение тренда принимает вид:

,

где , .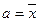

Пример Определить наличие тренда временного ряда, характеризующего расходы на канцелярские принадлежности в условном учебном заведении.

год	Расходы (тыс.руб)
	36.3
	39.7
	41.2
	43.5
	42.2
	43.1
	45.6
	47.2
	48.2
	50.5
	55.1
	53.4

Решение.

Разделим ряд на две равные части (т.к. в нем четное количество уровней). 1 часть: с 1996 г. по 2001 г.; 2 часть: с 2002 г. по 2007 г.

Количество уровней одинаково: ;

Вычислим выборочные средние частей временного ряда по формуле простой средней арифметической.

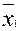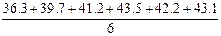= = 41;

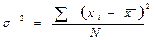
54.

Вычислим дисперсии по формуле:

( +

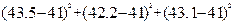+ ) = 5,99;

Аналогично, 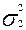= ∙119,7 = 19,95.

Вычислим экспериментальное значение критерия Стьюдента:

≈ 6,2.

Табличное значение t(0,01;8) = 3,36.

Так как экспериментальное значение больше табличного, тренд существует.

Ответ: Тренд существует.

Пример Выделить тренд методом скользящей средней и построить график.

t

x

Решение.

Рассчитаем средние значения по формулам:

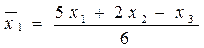Для удобства составим таблицу:

t	x	вычисление
		1/6∙(25+20-8) = 6.17	6.2
		1/3(5+10+8)= 7.67	7.7
		1/3(10+8+11) =9.7	9.7
		1/3(8+11+12) =10.3	10.3
		1/3(11+12+7) = 10
		1/3(12+7+14) = 11
		1/3(7+14+15) =12
		1/3(14+15+10) = 13
		1/3(15+10+18) = 14.3	14.3
		1/3(10+18+20) = 16
		1/3(18+20+15) = 17.7	17.7
		1/6(75+40-18) =16.17	16.2

Таким образом, сглаженный ряд имеет вид:

t
	6.2	7.7	9.7	10.3					14.3		17.7	16.2

Построим исходный и сглаженный ряды.

Пример. Написать уравнение линейного тренда и построить график.

t

x

Решение.

Уравнение линейной зависимости имеет вид:

,

где , .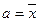

Вычислим параметры и b.

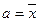= 1/12(5+10+8+11+12+7+14+15+10+18+20+15) = 12.08

Для вычисления b составим таблицу:

(медиана)

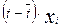
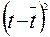
		−5.5	−27.5	30.25
		−4.5	−45	20.25
		−3.5	−28	12.25
		−2.5	−27.5	6.25
		−1.5	−18	2.25
		−0.5	−3.5	0.25
		0.5		0.25
		1.5	22.5	2.25
		2.5		6.25
		3.5		12.25
		4.5		20.25
		5.5	82.5	30.25
	∑		140.5

Уравнение тренда принимает вид:

, см.рисунок:

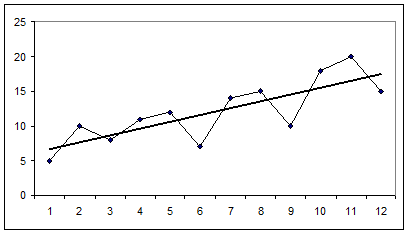
Дата добавления: 2015-05-10