IV Інтерполювання функцій

Приклад 1. За допомогою формули Лагранжа побудувати інтерполяційний многочлен для функції, що задана наступною таблицею

Таб.

xi	–2	–1
fi		–1	–1		–13

Обчислити значення в точці x=0,5.

Розв’язання. За формулою Лагранжа

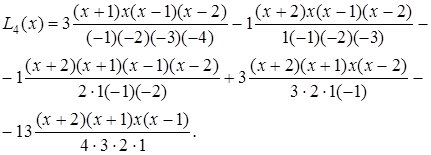
Далі

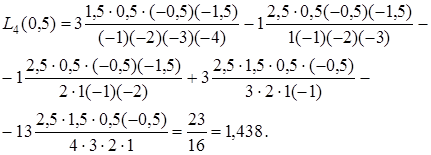
Приклад 2. Побудувати інтерполяційний многочлен за формулою Ньютона для функції, що задана таблицею (х), та обчислити значення в точці x=0,5.

Розв’язання. Таблиця розділених різниць для цих даних має вигляд

xi	fi
–2
		–4
–1	–1
	–1				–1
				–4
			–10
		–16
	–13

Тоді за формулою Ньютона

.

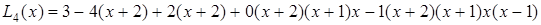Далі

.

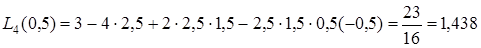Приклад 3. За допомогою інтерполяції обчислити e^0,15, якщо

xi	0.	0.1	0.2
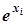
		1,10517	1,22140

Оцінити похибку.

Розв’язання. Позначимо . Тоді таблиця розділених різниць для даних в таблиці має вигляд

xi	fi
	1,0
		1,0517
0,1	1,105187		0,553
		1,1623
0,2	1,22140

Тому

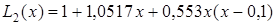
та

.

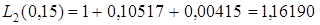Оцінка для похибки буде мати вигляд

,

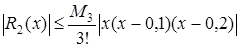де 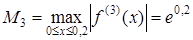. Тому

.

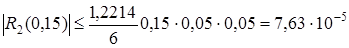Приклад 4. За значеннями 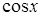в точках 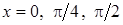знайти 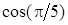. Оцінити похибку.

Розв’язання. Таблиця розділених рівнянь має вигляд

xi	fi
	1,0

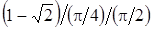
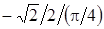
Приклад 5. а) Побудувати на проміжку [–1,1] многочлени Чебишева четвертого та п’ятого степеня з коефіцієнтом 1 при старшому степені. Обчислити їх відхилення від 0. Побудувати графіки.

Розв’язання. За рекурентною формулою

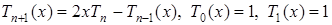
знаходимо

Шукані многочлени Чебишева мають вигляд

.

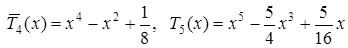За формулою відхилення від нуля такі

.

б) Побудувати на проміжку [0,1] многочлен Чебишева четвертого степеня з коефіцієнтом 1 при старшому степені. Обчислити її відхилення від 0.

Розв’язання. У многочлені Чебишева

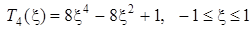
(див. попередню задачу) зробимо заміну змінної

.

При a= 0, b= 1 маємо x - 2 x- 1. Тоді многочлен Чебишева для проміжку [0,1] має вигляд

.

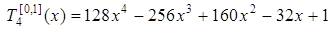Шуканий многочлен такий

.

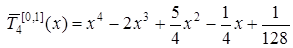Його відхилення від 0 дорівнює

.

Приклад 6. Оцінити похибку інтерполяції функції e^x на[0,1] многочленом четвертого степеня побудованим за вузлами.

Розв’язання. З оцінки залишкового члена інтерполяційної формули маємо

.

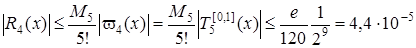Приклад 7. Скільки чебишевських вузлів інтерполяції необхідно вибрати, щоб похибка інтерполяції для функції не перевищувала e =10^–4.

Розв’язування. З оцінки залишкового члена інтерполяційної формули маємо

.

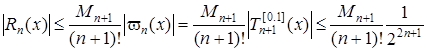Далі

.

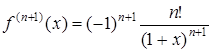Тому n шукаємо з умови

.

Підстановкою знаходимо, що

.

Таким чином треба вибрати 6 чебишевських вузлів.

Дата добавления: 2015-05-10