Непрерывный принцип Дирихле

Как правило, этот принцип применяется для нескольких чисел и их суммы. В общем виде для чисел он выглядит следующим образом:

"Если сумма n чисел больше S, то по крайней мере одно из этих чисел больше S/n".

По-другому его можно сформулировать так:

"Если среднее арифметическое нескольких чисел больше a, то хотя бы одно из этих чисел больше a";

или в терминах "зайцев":

"Если n кроликов съели m кг травы, то какой-то кролик съел не меньше m/n кг травы".

Кроме того, существует простая геометрическая интерпретация непрерывного принципа Дирихле:

"Пусть из некоторой точки на плоскости проведено N различных лучей; тогда угол между некоторыми двумя из них не менее 360°/N".

Понятно, что если рассматривать только углы между соседними лучами, то всего получится N углов (См. рисунок). В сумме они составляют полный угол, равный 360°. Следовательно,

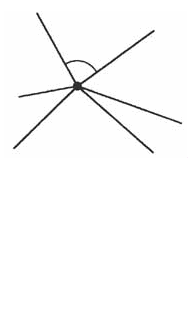по непрерывному принципу Дирихле градусная мера одного из этих углов не менее 360°/N (иначе их сумма будет меньше 360°).

Рассмотренный принцип называется непрерывным постольку, поскольку здесь числа (или градусные меры углов) могут принимать любое значение из некоторого промежутка, в то время как принцип Дирихле в обычном смысле оперирует с дискретным набором объектов ("зайцев") - было бы абсурдным предполагать, что в клетке может оказаться, скажем, два с половиной зайца.

Пример 17. На плоскости дано n попарно непараллельных прямых. Доказать, что найдутся две из них, угол между которыми не меньше 180°/n.

Указание. Достаточно перенести прямые параллельно самим себе так, чтобы все они проходили через одну точку. Из этой точки будет выходить 2n лучей, и теперь можно применить принцип Дирихле.

Пример 18. На полях шахматной доски 8×8 расставлены действительные числа, каждые два из которых отличаются не менее чем на 1/9. Доказать, что есть пара соседних (имеющих общую сторону) клеток, разность чисел в которых не меньше 1/2.

Решение Пусть A - наименьшее из выписанных на доске чисел, а B - наибольшее. Покажем, что B-A і7.

Запишем числа в порядке возрастания (заметим, что никакие два числа не равны):

x1 < x2 < x3 <... < x63 < x64    

(здесь x1 = A, x64 = B).

Тогда

B - A = x64 - x1 = (x64 - x63) +
+ (x63 - x62) +... + (x3 - x2) + (x2 - x1) і
і (1/9) + (1/9) +... + (1/9) = 63·(1/9) = 7.

Допустим теперь, что утверждение задачи неверно, т.е. в любой паре соседних клеток числа отличаются меньше чем на 1/2. Рассмотрим две клетки, в которых записаны числа A и B. Понятно, что, переходя из клетки в клетку, можно попасть из клетки A в клетку B, сделав не более 14 переходов. Самый худший случай, когда нужно сделать ровно 14 переходов, показан на рисунке (A, B - противоположные клетки). По предположению приращение на каждом переходе меньше 1/2. Поэтому B - A < 14·(1/2) = 7. Противоречие.

Дата добавления: 2015-05-10