Методические систематические погрешности нужно по возможности устранить или учесть путём введения специальных поправочных коэффициентов к измеряемой величине Х

Приборные систематические погрешности определяются по классу точности прибора. Существуют семь классов точности приборов - 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0.

Если класс точности на шкале прибора заключён в кружок (прибор нормирован по относительной погрешности), например, 0,5, то

DХ_сист = DХ_приб = 0,01^.К^.Х, (2а)

где К - класс точности прибора, Х - измеренное значение физической величины.

Если класс точности на шкале прибора не заключён в кружок (прибор нормирован по приведенной погрешности), то DХ_сист = DХ_приб = 0,01^.К^.Х^max, (2b)

где Х^max -верхний предел измерений прибора.

Если класс точности прибора не известен, то погрешность принимают равной половине цены наименьшего деления шкалы стрелочного прибора, и одного наименьшего деления шкалы цифрового прибора. Если стрелка прибора перемещается вдоль шкалы скачками, как например, у ручного секундомера, то приборную погрешность принимают равной цене деления, соответствующего одному скачку стрелки.

Для определения случайной погрешности измерения проводят многократно.

За наиболее достоверное значение непосредственно измеряемой физической величины Х принимают среднее из всех n измерений:

<X>= 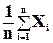. (3)

Стандартная случайная погрешность равна:

DХ_сл = t_an 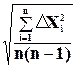, (4)

где DХ_i = |<X> - X_i| - абсолютная погрешность i -го измерения; t_an - коэффициент Стьюдента, зависящий от числа измерений n и от требуемой надёжности a получаемого результата, определяемый по специальной таблице (cм. ниже). При числе измерений n ³ 5 с надёжностью a=2/3 коэффициент Стьюдента t_an = 1.

Относительной погрешностью измерения величины Х называется величина:

dХ = 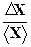. (5)

Истинное значение измеряемой величины Х с надёжностью a находится в интервале [<Х> - DХ, <Х> + DХ], где <Х> определяется формулой (3), а DХ - формулой (1) с подстановкой значений DХ_сист и DХ_сл, рассчитанных по формулам (2) и (4). Условно это записывают в виде:

X = <X> ± ΔX. (6)

При косвенных измерениях значение физической величины определяется путёмпрямых измерений других физических величин, а также использования известных параметров измерительной установки и справочных данных с дальнейшей подстановкой этих значений в рабочую формулу и соответствующих расчётов.

Например, Y = f (a,b,c,d), где a = <a> ± Da, b = <b> ± Db, c = <c> ± Dc, d = <d> ± Dd.

Наиболее близким к истинному значению будет:

Y =f (<a>, <b>, <c>, <d>), (7)

а стандартная погрешность DY принимается равной:

DY= 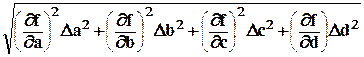. (8)

В простых случаях, когда, например, Y = a^a b^b c^g, удобно расчёт вести по формуле:

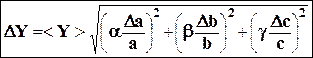. (9)

Истинное значение измеряемой величины Y находится в интервале [<Y> - DY, <Y> + DY ], где <Y> определяется формулой (7), а DY - формулой (8) или (9). Таким образом, результат может быть представлен в стандартной форме (6):

Y = <Y> ± DY.

При записи результата измерений в стандартной форме необходимо соблюдать

правила округления:

1-ое правило - погрешности DХ или DY округляются до двух значащих цифр, если первая цифра единица, и до одной значащей цифры во всех остальных случаях;

2-ое правило - средние значения измеряемых величин <Х> или <Y> округляются до последнего десятичного разряда, который используется при записи погрешности.

Коэффициенты Стьюдента t_an

n	a
0,5	0,6	0,7	0,8	0,9	0,95	0,99
	1,00	1,38	2,0	3,1	6,3	12,7	63,7
	0,82	1,06	1,3	1,9	2,9	4,3	9,9
	0,77	0,98	1,3	1,6	2,4	3,2	5,8
	0,74	0,94	1,2	1,5	2,1	2,8	4,6
	0,73	0,92	1,2	1,5	2,0	2,6	4,0
	0,72	0,90	1,1	1,4	1,9	2,4	3,7
	0,71	0,90	1,1	1,4	1,9	2,4	3,5
	0,71	0,90	1,1	1,4	1,9	2,3	3,4
	0,70	0,88	1,1	1,4	1,8	2,3	3,3
	0,68	0,85	1,0	1,3	1,7	2,0	2,6
¥	0,67	0,84	1,0	1,3	1,6	2,0	2,6

Дата добавления: 2015-05-10