Система лінійних рівнянь. Матричний метод

Решение.

Исходные данные, выписанные из АЕ 1988 года.

S_o = 5^h 43^m 21.3849 ^s

ΔT = 57^s

α_o= 17^h 39^m 23.669 ^s

δ_o= - 23º21´29.91´´

υδ_o= -5.447²

E_o = 12^h 03^m 57.716 ^s

υE_o = -1.2218^s

Задача 1.

Dn = 18^h49^m24.5^s; λ= 03^h37^m31.66^s

M = Dn – (n+k)

n = 4^h k = +1^h

M = 18^h49^m24.5^s 5^s – 5^h = 13^h49^m24.5^s

Tn = Dn – k

Tn = 18^h49^m24.5^s -1^h = 17^h49^m24.5^s

To = Tn – n = M

To = 17^h49^m24.5^s – 4^h = 13^h49^m24.5^s

m=M+ λ

m = 13^h49^m24.5^s + 05^h57^m34.87^s = 19^h46^m59.37

UT = 13^h49^m24.5^s

Задача 2.

ET = UT + ΔT

h =(ET)^h.ддд;

δ = δ_o + υδ_o´h;

M	13^h49^m24.5^s
ΔT	57^s
ET	13^h50^m21.5^s
h	13,839^h.ддд
υδo	-5,447²
υδo´h	-75,381²=-1¢15,381²
δo	- 23º21´29.91²
d	- 23º22´45,29²

a = a_o + υa0´h;

υ_αo= 9.856^s - υ_Eo=9.856^s + 1.2218^s =11.0778^s

M	13^h49^m24.5^s
ΔT	57^s
ET	13^h50^m21.5^s
H	13,839^h.ддд
υαo	11,078^s
uα0´h	153.308^s =2^m33.31^s
αo	17^h 39^m 23.669 ^s
a	17^h 41^m 56.98 ^s

E= E*- ΔT´μ= Eo+ υ_Eo´h- ΔT´μ

μ = 0.00273791

ΔT* μ = 57^s *0.00273791 = 0.156^s

M	13^h49^m24.5^s
ΔT	57^s
ET	13^h50^m21.5^s
h	13,839^h.ддд
υEo	-1,2218^s
υEo´h	-16,908^s
Eo	12^h 03^m 57.716^s
E*	12^h 03^m 40.808^s
ΔT´μ	-0.156^s
E	12^h 03^m 40.65^s

Задача 3.

s = S+l=So+M+Mμ+λ

s = s_o+m+mμ

μ = 0.00273791

s_o= So- λμ

s = s_o+(M+ λ)+(M+ λ) μ

s_o+(M+ λ)+(M+ λ) μ= So+M+Mμ

s_o= So+M+Mm+λ-M-λ-Mm-λm=So-λm

So	5^h 43^m 21,385 ^s
M	9 09 34,5
M*μ	0 01 30,28
S	14 54 56,16
λ	5 57 34,87
s	20 52 01,03

So	5^h 43^m 21,385 ^s
λμ	0 00 58,74
so	5 42 22,64
m	15 07 09,37
m*μ	0 02 29,02
s	20 52 01,03

Задача 4.

t_, = s-α_,

t_, = E+m

t_, = 20^h 52^m01.03^s - 17^h 41^m 05.319^s =3^h 10^m 55.71^s

t_, = 12^h 03^m 46.341^s + 15^h 07^m 09.37^s = 3^h 10^m 55.71^s

Задача 5.

M = (S – So) – (S-S₀)ν

m = (s – s_o) – (s – s_o) ν

S = So + M + M μ=s-l

ν = 0.00273043

S = s – l

s=20^h52^m01.03^s

l=5^h 57^m 34.87^s

S=14^h 54^m 26.16^s

S = 14^h54^m26.16^s

S₀= 5^h43^m21.38^s

S- S₀= 9^h11^m04.78^s

(S-S₀)ν= 01^m 30.28 ^s

M =9^h 09^m 34.5^s

m = (s – s_o) – (s – s_o) ν

s = 20^h52^m01.03^s

s_o= 5^h42^m22.64^s

s – s_o= 15^h09^m38.39^s

(s – s_o) ν= 02^m29.02^s

m = 15^h07^m09.37^s

m = 15^h 07^m 09.37^s

Задана система 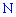лінійних алгебраїчних рівнянь (СЛАР) з 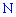невідомими 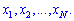,коефіцієнтами при яких є елементи матриці 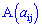, а вільними членами є числа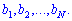

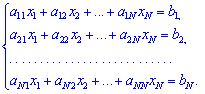
Позначимо через 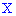– матрицю-стовпець невідомих, через – матрицю-стовпець вільних членів. Тоді попередю систему рівнянь можна записати у вигляді матричного рівняння:

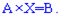
Якщо квадратна матриця має відмінний від нуля визначник 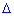, то для неї існує обернена 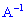. Помноживши зліва в цьому рівнянні на 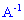, одержимо

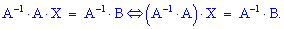
Враховуючи, що 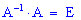і 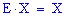, одержимо матричний розв'язок системи

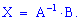
Знаходження матричного розв'язку називається матричним способом розв'язування системи лінійних алгебраїчних рівнянь (СЛАР).

---------------------------------------------------------------

Приклад 1.

Розв'язати СЛАР матричним методом.

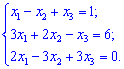
Розв'язок.

Позначимо матрицю і вектори

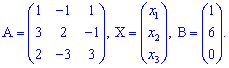
Матричний розв'язок системи алгебраїчних рівнянь шукаємо за формулою

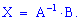
Для знаходження оберненої матриці 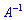обчислимо визначник

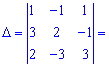
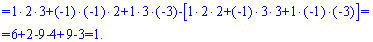
Оскільки 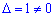, то задана система рівнянь сумісна і має єдиний розв'язок.

Знайдемо транспоновану матрицю

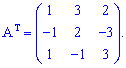
Знайдемо алгебраїчні доповнення до елементів заданої матриці:

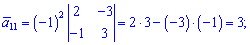
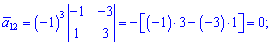
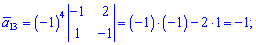
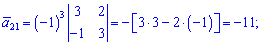
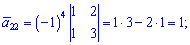
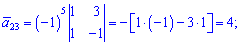
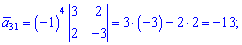
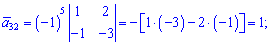
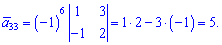
Обернену матрицю обчислюємо за формулою

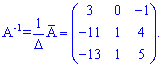
Знайдемо розв'язок СЛАР

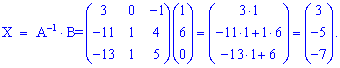
Розв'язок СЛАР:

x1= 3, x2= -5, x3= -7

Дата добавления: 2015-05-10