Мосты переменного тока

Метод измерительного моста переменного тока находит широкое применение для измерения омического сопротивления, емкости, танген­са угла потерь, индуктивности, добротности.

В отличие от мостов постоянного тока здесь одну диагональ моста включен источник переменного напряжения (генератор низкой частоты), в другую - нулевой индикатор переменного напря­жения, плечи моста - двухполюсники с полным сопротивлением Z (рис.10.2).

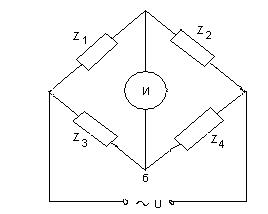
Рисунок 10.2 – Схема моста переменного тока

Равновесие моста достигается при условии ра­венства произведений комплексных сопротивлений противоположных плеч:

Z₁Z₄ = Z₂Z₃. (10.3)

В показательной форме равенство будет иметь вид

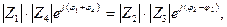(10.4)

где 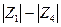- модули полных сопротивлений плеч; φ₁ – φ₄ – фазовые сдвиги между током и напряжением в соответ­ствующих плечах.

Равенство (10.4) представим в виде двух равенств:

-равенство произведений модулей комплексных сопротивлений противолежащих плеч:

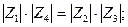(10.5)

- равенство сумм аргументов комплексных сопротивлений противоположных плеч:

(10.6)

Равенства (10.5) и (10.6) определяют условия равновесия моста. Они показывают, что мост переменного тока нужно уравновешивать ре­гулировкой активной и реактивной составляющих плеч, т.е. равновесие осуществляется по модулям и фазам. При этом уравнения (10.5) и (10.6) равносильны и оба обязательны для достижения равновесия мо­ста. Условие (10.6) указывает, при каком расположении плеч в зависи­мости от их характера можно уравновесить схему. Если смежные плечи, например третье и четвертое (рис.10.2), имеют чисто активные со­противления R₃ и R₄, т.е. φ₃ = φ₄ = 0, то два других смежных плеча могут иметь или индуктивный, или емкостный характер. Если противо­положные плечи чисто активные, то одно из двух других сопротивлений должно быть индуктивным, а другое – емкостным.

При алгебраической форме представления комплексного сопроти­вления

Z = R + jX,

где R – вещественная часть, представляющая активную составляющую; X – мнимая часть, представляющая реактивную составляющую.

В алгебраической форме равенство (10.3) примет вид

(R₁ + jX₁)(R₄ + jX₄) = (R₂ + jX₂)(R₃ + jX₃) (10.7)

Это равенство обеспечивается при одновременном выполнении равенства активных и реактивных частей, т.е.

real: R₁R₄ – X₄X₁ = R₂R₃ – X₂X₃ и Im: R₁X₄ + R₄X₁ = R₂X₃ + R₃X₂.

Рассмотрим мост для измерения емкости и угла потерь конденсаторов (рис.10.3).

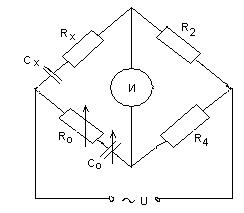
Рисунок 10.3 – Схема моста для измерения емкости

Два его плеча составлены из магазинов сопротивлений R₂ и R₄. Третье плечо образовано последовательно соединенными образцовыми конденсатором С_о и переменным резистором с малым сопротивлением R_o. В четвертое плечо включен измеряемый конденсатор С_х, сопротивление потерь в котором R_x.

Полные сопротивления плеч моста равны:

Подставив в формулу равновесия моста (10.3) эти значения, получим

Приравняв отдельно вещественные и мнимые части, получим

(10.8)

Из анализа векторной диаграммы цепи R_xC_x следует, что угол δ_х, дополняющий до 90^о φ_х, определяется как

tg δ_х = ωR_xC_x.

Уравновешивание моста переменного тока для измерения индуктивности рассмотрим на примере схемы, представленной на (рис.10.4).

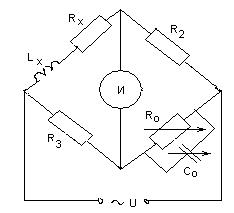
Рисунок 10.4 – Схема моста для измерения индуктивности

Здесь для измерения индуктивности L_x используют образцовый конденсатор С_о, включенный в плечо, противоположное плечу с измеряемой индуктивностью. Параллельно с конденсатором С_о включен резистор R_o. В остальные плечи включены магазины сопротивлений R₂ и R₃.

Полные сопротивления плеч равны

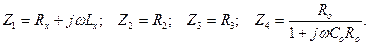
Равновесие моста согласно (10.2) определяется как

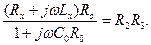
Отсюда следует, что

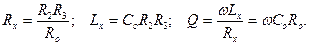(10.9)

На основании изложенного можно заключить, что для мостов, у которых два плеча содержат только активные сопротивления, а два других – реактивные (рис.10.3 и 10.4), справедливы следующие утверждения:

- если активные сопротивления находятся в смежных плечах (рис.10.3) R₂ и R₄ и φ₂ = φ₄ = 0, то два других плеча должны содержать сопротивления одного характера (индуктивного или емкостного), что обеспечивает выполнение условия φ₁ = φ₃;

- если активные сопротивления расположены в противоположных плечах (рис.10.4) R₂ и R₃ и φ₂ = φ₃ = 0, то характер сопротивлений двух других плеч должен быть противоположным, что обеспечивает выполнение условия φ₁ = -φ₄.

Погрешности измерений параметров цепей с использованием рассмотренных мостов составляет сотые доли % от измеряемой величины. Они обусловлены следующими причинами:

- погрешностью значений образцовых элементов моста;

- влиянием паразитных связей между элементами схемы;

- влиянием нестабильностью параметров элементов схемы;

- нестабильностью амплитуды и частоты источника переменного напряжения.

Дата добавления: 2015-05-10