Інші нормальні форми

Існують і інші нормальні форми, але вони сьогодні знаходять обмежене застосування. Перша нормальна форма встановлює умову: кожний компонент кожного атрибута має бути атомарним.

Друга нормальна форма – різновид третьої нормальної форми, який дозволяє наявність транзитивних FD, але забороняє існування нетривіальної FD із лівою частиною, що є підмножиною ключа.

Більш поширеною є третя нормальна форма, яка дещо пом’якшує умову BCNF. Вона має наступні визначення.

• Відношення R задовольняє 3NF, якщо виконується умова: Усякий раз, коли для відношення R існує деяка нетривіальна FD (А₁ , А₂ ,. А_n) → В, відповідна множина (А₁ , А₂ ,. А_n) представляє суперключ для R, або В є членом деякого ключа.
• 3NF має і таке визначення: “Для кожної нетривіальної FD повинна виконуватися одна із умов – або атрибути її лівої частини представляють собою суперключ, або атрибути її правої частини входять до складу первинного ключа відношення R.

Четверта нормальна форма (4NF) при побудові реляційних відношень враховує те, що причиною збитковості може бути існування зв’язків між атрибутами. Як позбутися такої аномалії, вказує 4NF. Дуже часто подібна збитковість виникає при спробі представити у рамках одного відношення дані декількох зв’язків типу “багато до багатьох”.

Визначення багатозначної залежності.

Багатозначна залежність (multyvalued dependency – MVD) – це твердження, деяка множина атрибутів відношення R не залежить від другої множини атрибутів. Але більш строге формулювання умови MVD наступне.

· Для кожної пари кортежів t і u відношення R, які співпадають у всіх атрибутах
(А₁ , А₂ ,. А_n), можна знайти у R деякий кортеж ν, співпадаючий:

а) з кортежами t і u в атрибутах (А₁ , А₂ ,. А_n);

b) з кортежем t в атрибутах (В ₁ , В₂, В_m);

с) з кортежем u у всіх інших атрибутах відношення R, які не належать множині
(А₁ , А₂ ,. А_n), ні множині (В ₁ , В₂, В_m)

На рис.6 показано, як кортеж ν може співвідноситися із кортежами t і u, зберігаючи у силі умову MVD.

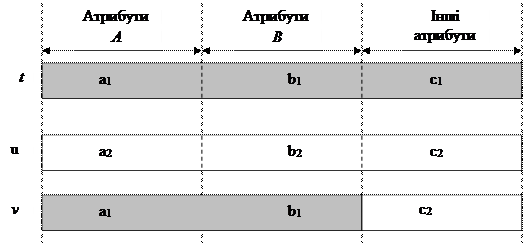Рис.6. Багатозначна залежність гарантує існування кортежу ν.

Взаємовідносини нормальних форм.

Якщо відношення R з певними FD задовольняє умові 4NF, то воно задовольняє умовам BCNF і 3NF. Якщо відношення R з певними FD задовольняє умові BCNF, то воно відповідає і 3NF. На рис.7. відображена вкладеність нормальних форм, а їх властивості на рис.8.

4NF Þ BCNF Þ 3NF

Рис.7. Вкладеність нормальних форм

Властивість	Забезпечення властивості у нормальній формі
3NF	BCNF	4NF
Відсутність надлишковості	У більшості випадків	Так	Так
Відсутність надлишковості із-за MVD	Ні	Ні	Так
Зберігання умов FD	Так	Не завжди	Не завжди
Зберігання умов MVD	Не завжди	Не завжди	Не завжди

Рис.8. Властивості нормальних форм і відповідних результатів декомпозиції

Створений набір відношень логічної моделі БД повинен бути перевірений на коректність об’єднання атрибутів у кожному відношенні. Перевірка виконується шляхом застосування до кожного відношення процедури послідовної нормалізації. Нормалізація гарантує, що отримана модель не буде мати протиріч і буде мати мінімальну збитковість. Атрибути в результаті нормалізації будуть згруповані відповідно до існуючих між ними логічних зв’язків. Для забезпечення коректності логічної моделі, у разі виявлення відношень, які не відповідають вимогам нормалізації, необхідно повернутися на попередні етапи проектування і перебудувати помилково створені елементи моделі.

Правила формування нормальних форм

Нормальні форми	Приклад
1НФ	R(ABCD) – відношення A, B, C, D – атомарні атрибути
2НФ	R(AB CD) – відношення, AB – ключ, AB → CD, неможливі залежності: A → CD, A → C, A → D, B → CD, B → C, B → D
3НФ	R(AB CD) – відношення, AB – ключ, AB → CD, неможливі залежності: C → D, D → C
НФБК	R(AB CD) – відношення, AB – ключ, AB → CD, неможливі залежності: C → A, C → B, D → A, D → B, C → AB, D → AB
4НФ	R(A BC) – відношення, A → → B, A → C, неможливі залежності: A → → C
5НФ	R(ABC) – вихідне відношення, результат декомпозиції: R1(AB), R2(AC), R3(BC)

Дата добавления: 2015-05-10