Физическая химия поверхностных явлений

ТЕМА № 10

Книги

Заказы

Продавцы

Покупатели

Имя поля	Тип	Длина	Индекс
Код покупателя	Счетчик		Да
Фамилия	Текстовый
Имя	Текстовый
Отчество	Текстовый
Город	Текстовый
Адрес	Текстовый
Страна	Текстовый

Имя поля	Тип	Длина	Индекс
Код продавца	Счетчик		Да
Фамилия	Текстовый
Имя	Текстовый
Отчество	Текстовый
Должность	Текстовый
Дата приема	Дата/время
Оклад	Денежный

Имя поля	Тип	Длина	Индекс
Код заказа	Счетчик		Да
Код продавца	Числовой
Код покупателя	Числовой
Код книги	Числовой
Дата получения	Дата/время
Дата отправки	Дата/время
Количество	Числовой

Имя поля	Тип	Длина	Индекс
Код книги	Счетчик		Да
Автор	Текстовый
Название	Текстовый
Издательство	Текстовый
Серия	Текстовый
Год издания	Числовой
Цена	Денежный

Приложение 3. Схемы данных БД «Книги»

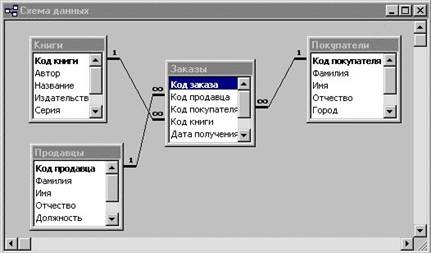
[1] Структура БД «Книги» приведена в приложении 2.

Теоретический материал к занятию:

К поверхностным явлениям относятся процессы, происходящие на границе раздела фаз; они обусловлены особенностями состава и структуры поверхностей.

Образование поверхности раздела фаз требует совершения работы, следовательно, оно сопровождается увеличением свободной энергии системы. В поверхностном слое накапливается некоторый избыток энергии — поверхностная энергия Гиббса Gs, пропорциональная площади поверхности раздела фаз S:

Gs = σS

где σ — коэффициент поверхностного натяжения, т. е. работа образования единицы поверхности. Коэффициент поверхностного натяжения также численно равен силе, приложенной к единице длины контура, ограничивающего поверхность, и направленной вдоль этой поверхности перпендикулярно контуру; dim σ = МТ-2, единица измерения — джоуль на квадратный метр (Дж/м2) или ньютон на метр (Н/м). Следует отметить, что коэффициент поверхностного натяжения часто называют поверхностным натяжением.

Самопроизвольное уменьшение свободной поверхностной энергии Gs в однокомпонентных системах возможно только за счет уменьшения площади поверхности раздела фаз. В многокомпонентных системах уменьшение Gs возможно также за счет уменьшения величины поверхностного натяжения в результате самопроизвольного перераспределения молекул компонента между объемом фазы и поверхностью раздела. Это явление называется адсорбцией.

Границы раздела фаз газ — жидкость и жидкость — жидкость принято называть подвижными, а границы газ — твердое тело, жидкость — твердое тело, твердое тело — твердое тело — неподвижными. Ниже будут рассмотрены адсорбционные процессы в таких системах, в которых жидкость представлена водным раствором.

В зависимости от природы растворенного вещества (компонента) возможно увеличение или уменьшение его концентрации в поверхностном слое.

Положительно адсорбирующиеся вещества уменьшают коэффициент поверхностного натяжения водной фазы, их называют поверхностно-активными веществами (ПАВ).

Молекулы ПАВ имеют характерные черты строения: они дифильны, т. е. содержат гидрофобные и гидрофильные фрагменты, и асимметричны. К ПАВ относятся одноатомные спирты, одноосновные карбоновые кислоты, амины, эфиры и др.

Поверхностно-неактивные вещества (адсорбирующиеся отрицательно) либо не изменяют коэффициент поверхностного натяжения водной фазы, либо незначительно его увеличивают. К ним относится большинство неорганических веществ (кислоты, щелочи, соли).

Количественной мерой адсорбции служит величина адсорбции Г (гамма);dimГ = L-2N, единица измерения — моль на квадратный метр (моль/м2). Связь между величиной адсорбции в интервале концентраций и коэффициентом поверхностного натяжения устанавливает уравнение Гиббса:

с_ср ds

Г = - ¾ × ¾¾,

RT dc

где Δσ — приращение коэффициента поверхностного натяжения, соответствующее приращению концентрации Δc;

c_ср — среднее значение концентрации раствора в ин-тервале концентраций.

Для ПАВ при увеличении концентрации (Δс > 0) наблюдается уменьшение коэффициента поверхностного натяжения (Δσ < 0). Величину - (dσ/dc) называют по-верхностной активностью; она характеризует способность вещества изменять величину поверхностного натяжения раствора. В соответствии с правилом Траубе увеличение длины цепи молекул ПАВ в данном гомологическом ряду (карбоновые кислоты, спирты, амины) вызывает увеличение поверхностной активности в 3—3,5 раза при переходе к каждому последующему гомологу.

Величина адсорбции зависит от природы соприкасающихся фаз, природы и концентрации растворенного вещества. С увеличением концентрации ПАВ величина адсорбции сначала резко возрастает, но затем дальнейшее увеличение концентрации ПАВ вызывает незначительное увеличение этой величины и в конце концов величина адсорбции перестает зависеть от концентрации ПАВ

По теории Лэнгмюра предельной адсорбции Гмакс соответствует образование насыщенного (мономолекулярного) адсорбционного слоя, что позволяет рассчитать площадь S поперечного сечения, занимаемую одной молекулой, и ее длину l:

S = ¾¾¾,

Г_максN_A

Г_максМ

l = ¾¾¾

r

где N_A - постоянная Авогадро,

r - плотность растворенного вещества,

М – молярная масса.

Величина адсорбции уменьшается при увеличении температуры, что обусловлено усилением интенсивности теплового движения молекул и разупорядочиванием структуры поверхностного слоя.

Причиной адсорбции на поверхности твердых тел является нескомпенсированность силовых полей молекул, находящихся в зонах деформации регулярно устроенной поверхности. Такие зоны называют активными центрами; адсорбцию, проходящую на них, разделяют на физическую и химическую (хемосорбция). Любая поверхность, даже хорошо отшлифованная, имеет свой микрорельеф — совокупность впадин и выступов. Физическая адсорбция обусловлена межмолекулярным взаимодействием (ван-дер-ваальсовым; в ряде случаев — за счет образования водородных связей) и проходит, как правило, на активных центрах, находящихся во впадинах микрорельефа поверхности. Центры химической адсорбции находятся в основном на выступах микрорельефа; при хемосорбции устанавливаются химические связи между атомами, входящими в состав активного центра, и атомами адсорбирующегося вещества.

Различия между физической адсорбцией и хемосорбцией заключаются в следующем:

1) значения стандартных энтальпий хемосорбции (порядка 80—800 кДж/моль) значительно выше таковых величин физической адсорбции (8—20 кДж/моль), значения стандартных энтальпий хемосорбции близки ΔH° химических реакций;

Классический пример адсорбции на твердом теле — поглощение различных газов активированным углем. Твердое тело, на поверхности которого происходит адсорбция, называют адсорбентом, а само адсорбирующееся вещество — адсорбтивом. Практически процесс поглощения вещества поверхностным слоем часто дополняется поглощением адсорбтива всем объемом твердого тела — абсорбцией, суммарный процесс (адсорбция + абсорбция) называют в таком случае просто сорбцией. Сорбция — обратимый процесс. Удаление сорбированного вещества называют десорбцией.

Количественно адсорбция на подвижной (Г) и неподвижной (a) границах раздела описывается уравнением Ленгмюра:

c

a = a_макс¾¾

a + с

где а_макс - величина предельной адсорбции, она достигается при занятии всех активных центров адсорбента; dim a = М-1N, единица измерения - моль/г; a - постоянная величина, равная отношению констант скоростей десорбции и адсорбции, имеющая размерность концентрации.

В некоторых случаях для описания адсорбции используют эмпирическое уравнение Фрейндлиха:

a = Kcⁿ

где n и K - константы, определяемые экспериментально.

Величину адсорбции из раствора на твердом адсорбенте экспериментально определяют по изменению концентрации растворенного вещества после завершения адсорбции, т. е. установления адсорбционного равновесия по формуле:

(c_o-c)V

a = ———

m

где co и с — исходная и равновесная концентрация раствора соответственно, моль/л;

V - объем раствора, из которого производилась адсорбция, л; m — масса адсорбента, г.

Константы уравнения Ленгмюра определяются экспериментально по графику 1/a = f(1/c).

Величина адсорбции значительно зависит от удельной поверхности адсорбента. Удельная поверхность адсорбента Sуд равна отношению площади его поверхности к объему. Она обратно пропорциональна размеру частиц и зависит от их формы. При дроблении и измельчении твердых тел величина их удельной поверхности увеличивается вплоть до значений, достигающих тысячи квадратных метров на куби-ческий сантиметр твердого тела. Чем больше удельная поверхность адсорбента, тем больше имеется активных центров и, следовательно, больше величина адсорбции.

Величина адсорбции зависит от природы адсорбента и адсорбтива: чем ближе по полярности адсорбент и адсорбтив, тем полнее происходит адсорбция.

При адсорбции из растворов большое значение имеет и полярность растворителя. Наибольшей склонностью к адсорбции обладают вещества с полярностью, промежу-точной между полярностями контактирующих фаз. Из водных растворов ПАВ хорошо адсорбируются неполярными адсорбентами (в том числе активированным углем), а на полярных адсорбентах (карбонаты, алюмосиликаты, оксиды) ПАВ хорошо адсорбируются из неполярных сред. В основе этих явлений лежит конкуренция между молекулами адсорбтива и растворителя за активные центры адсорбента.

В соответствии с правилом Ребиндера адсорбция идет в сторону выравнивания полярностей контактирующих фаз и тем сильнее, чем больше начальная разность полярностей.

Адсорбция из растворов электролитов осложняется ярко выраженным характером электростатических взаимодействий, приводящих к образованию на поверхности адсорбента двойного электрического слоя (ДЭС).

Различают следующие разновидности адсорбции из растворов электролитов:

1) эквивалентную;

2) обменную;

3) избирательную.

При эквивалентной адсорбции катионы и анионы адсорбируются в таких количествах, которые соответствуют нулевому суммарному заряду. Эквивалентную адсорбцию формально можно рассматривать как адсорбцию неэлектролита, так как при этом не возникают отрицательно или положительно заряженные поверхности.

Обменная адсорбция заключается в обмене ионами между адсорбентом и раствором: адсорбенты, способные к обмену катионов, называются катионитами;

анионов — анионитами.

При избирательной адсорбции на поверхности адсорбента накапливаются либо катионы, либо анионы. Ионы противоположного заряда сохраняют при этом относительную подвижность в растворе. Таким образом, в результате избирательной адсорбции возникают заряженные поверхности. В соответствии с правилом Панета — Фаянса из раствора преимущественно адсорбируются ионы, которые входят в состав кристаллической решетки твердой фазы, или им изоморфные. Так, например, из раствора, содержащего хлорид бария и нитрат стронция, на поверхности кристаллов сульфата бария адсорбируются ионы бария (входят в кристаллическую решетку) и ионы стронция (изоморфны ионам бария); поверхность твердой фазы сульфата бария приобретает положительный заряд. Если тот же адсорбент контактирует с раствором сульфата натрия и перманганата калия, то избирательно на его поверхности адсорбируются сульфат-ионы (входят в кристаллическую решетку) и перманганат-ионы (изоморфны сульфат-ионам). Поверхность твердой фазы приобретает отрицательный заряд. Адсорбция ионов зависит от радиуса иона (она тем больше, чем больше радиус иона) и величины его заряда (многозарядные ионы адсорбируются лучше).

До решения задач необходимо:

I. Выучить определения основных понятий:

1) адсорбция, предельная адсорбция;

2) поверхностное натяжение;

3) коэффициент поверхностного натяжения;

4) поверхностно-активные и поверхностно-неактивные вещества;

5) поверхностная активность;

6) адсорбент, адсорбтив;

7) правило выравнивания полярностей Ребиндера.

II. Разобрать следующие вопросы:

1) подвижная и неподвижная поверхность раздела фаз;

2) связь между величиной адсорбции и коэффициентом поверхностного натяжения (уравнение Гиббса);

3) изменение величины поверхностной активности в гомологическом ряду (правило Траубе);

4) связь величины предельной адсорбции с площадью поперечного сечения и осевой длины молекулы;

5) уравнение изотермы адсорбции Ленгмюра.

III. Обратить внимание на:

1) размерность величин адсорбции на подвижной границе фаз и на твердых адсорбентах.

Примеры решения типовых задач

Пример 1

Расчет величины поверхностной активности ПАВ по изменению поверхностного натяжения; расчет величины поверхностной активности гомолога по правилу Траубе, расчет величины адсорбции ПАВ в заданном интервале концентраций.

Поверхностное натяжение водного раствора пентанола с концентрацией 0,030 моль/дм³ равно 55,3 10^-3 Н/м при 298 К. Оцените величину адсорбции бутанола из раствора с концентрацией 0,015 моль/дм³ при той же температуре.

Решение. Найдем поверхностную активность пентанола g(С5Н11OН) в интервале концентраций C1 = 0 (т.е. чистый растворитель) - C2= 0,030 моль/дм³:

g(С5Н11OН) = -

- коэффициент поверхностного натяжения воды, справочная величина (табл.11.02.).

В соответствии с правилом Траубе поверхностная активность бутанола, предшествующего члена гомологического ряда предельных одноатомных спиртов, будет в тех же условиях примерно в 3,2 раза меньше:

g(С4Н9OН) =

Поскольку концентрация раствора бутанола равна 0,015 моль/дм³ является серединой интервала, в котором рассчитывалась поверхностная активность, величина адсорбции из этого раствора рассчитывается по уравнению Гиббса:

Г(C4H9OH) =

g(С5Н11OН) =

g(С4Н9OН) =

Г(С4Н9OН) =

Ответ: величина адсорбции бутанола приблизительно равна 1 10-6 моль/м2.

Пример 2

Расчет длины и площади поперечного сечения молекулы по величине предельной адсорбции.

Площадь поперечного сечения молекулы пальмитиновой кислоты равна 2,1×10^-19м². Определите величину предельной адсорбции пальмитиновой кислоты на границе бензольный раствор-воздух. Вычислите объем раствора, содержащего 4,24 г кислоты в 1 л бензола, требуемый для покрытия монослоем (после испарения бензола) 1,5 м² водной поверхности.

Решение. Величину предельной адсорбции данного вещества рассчитывают по уравнению:

Г_max =

Для покрытия площади S монослоем молекул с площадью поперечного сечения S мол требуется S/S мол молекул. Количество вещества, соответствующее этому числу молекул, рассчитывают по соотношению:

n = : NA

Молярная концентрация имеющего раствора пальмитиновой кислоты равна:

С_(к-ты) =

Требуемый объем раствора равен: Vp = /с

Г max = = 7,9 10-6моль/м2

n = = 1,19 10-5моль

с (к-ты) = = 1,66 10-2моль/дм3

V =

Ответ: Г max = 7,9 10-6 моль/м² Vр = 0,715 мл

__________________________________________________________________________________

Пример 3

Расчет величины адсорбции по уравнению Ленгмюра при заданных константах.

Экспериментально установлено, что максимальная величина адсорбции ПАВ (M_r = 60) некоторым адсорбентом составляет 5,0×10^-3 моль/г; величина a равна 0,06 моль/дм³. Сколько граммов вещества адсорбировалось из раствора с равновесной концентрацией 0,1 моль/дм³ двумя граммами данного адсорбента?

Решение. По уравнению Ленгмюра рассчитывают величину адсорбции ПАВ:

а = a max

Количество адсорбированного вещества на адсорбенте массой 2 г будет в 2 раза больше.

Масса адсорбированного вещества будет равна:

m (ПАВ) = n (ПАВ) М(ПАВ)

а = = 3,1 10-3моль/г

n(ПАВ) = 3,1×10-3моль/г 2 г = 6,2 10-3моль

m(ПАВ) = 6,2×10-3моль 60 г/моль = 0,37 г

Ответ: масса адсорбированного вещества равна 0,37 г.

Пример 4

Расчет величины адсорбции на твердом адсорбенте по изменению концентрации адсорбтива.

Раствор уксусной кислоты объемом60 см³ раствора уксусной кислоты с концентрацией 0,1 моль/дм³ взболтали с 2 г адсорбента. После достижения равновесия пробу раствора объемом 10 см³ оттитровали раствором гидроксида натрия с = 0,05 моль/дм³. На титрование затрачено 15,0 см³ титранта. Вычислите величину адсорбции уксусной кислоты.

Решение. Равновесная концентрация уксусной кислоты равна (по результатам титрования):

(СН3СООН) =

Величину адсорбции рассчитывают по:

а =

с(СН3СООН) = = 0,075 моль/см3

а =

Ответ: а (СН3СООН) = 6,25 10-4моль/г

Задания для самостоятельной работы из «Сборника задач и упражнений по общей химии».

10.31; 10.35; 10.40; 10.46,10.52; 10.54

Лабораторная работа 9.3

Дата добавления: 2015-05-10