Основные понятия. - освоение методики оценки случайной погрешности прямых и косвенных измерений;

Задачи

Цель

- освоение методики оценки случайной погрешности прямых и косвенных измерений;

- определение действительного значения измеряемой величины контролируемого параметра.

- определить среднеарифметическое значение измеряемой величины;

- определить размах измеряемой величины;

- определить математическое ожидание измеряемой величины;

- определить среднеквадратичное отклонение измеряемой величины;

- определить дисперсию измеряемой величины;

- определить доверительный интервал измеряемой величины.

Случайные погрешности – погрешность измерений, величина которых меняется под действием постоянно изменяющихся, трудно поддающихся учету факторов.

Грубые погрешности – погрешности, вызванные неисправностью средств измерений или ошибками наблюдателей (исполнителей).

Положения теории случайных ошибок:

- результаты независимых измерений некоторой величины (параметра) X₁, X₂…X_n свободны от грубых и систематических ошибок;

- при большом числе измерений случайные погрешности одной величины, но разного знака появляются одинаково часто;

- большие погрешности измерений встречаются реже, чем малые;

- при бесконечно малом числе измерений действительное значение определяемого параметра равно среднеарифметическому всех измерений;

- появление того или иного результата измерений как случайного события описывается законом нормального распределения.

4. Расчет

1. Результаты измерений, полученные при операционном контроле качества (испытание цементобетонных балок 20х20х60см на растяжение при изгибе), преобразую в статистический ряд, располагая в порядке возрастания (МПа):

3,87; 3,87; 3,88; 3,88; 3,94; 3,99; 4,02; 4,08; 4,08; 4,13; 4,52; 4,52; 4,53; 4,54; 4,56; 4,60; 4,61; 4,61; 4,62; 4,62; 4,62; 4,68; 4,74; 4,74; 4,79; 4.82; 4,83; 4,85; 4,85; 4,88; 4,92; 4,98; 5,16; 5,31; 5,44; 5,49; 5,50; 5,83; 5,97.

2. Среднеарифметическое значение результатов измерений (в качестве оценки математического ожидания):

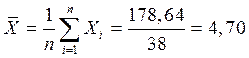
X_i – результаты независимых измерений,

N – общее число (количество) измерений.

3. Абсолютные погрешности ε_i (см. табл. 1), приняв за действительное значение:

ε_i= Х_i-

и абсолютные крайние погрешности:

минимальная ε_min= -Х_min =4,70-3,87 =0,83

максимальная ε_max= Х_max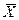^- =5,97-4,70= 1,27

4. Среднеквадратичное отклонение:

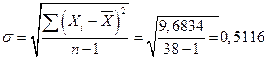
5. Относительные погрешности:

минимальная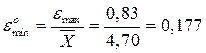

максимальная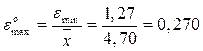

6. Пренебрежимо малую погрешность измерения, принимая ε_пред= :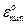

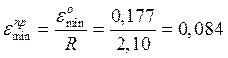
R - размах, который указывает на разницу крайних измерений контролируемого параметра (статистического ряда):

R=X_max-X_min =5,97-3,87=2,10

табл. 1

№ п/п	Xi		εi	ε^2i
	3,87	4,70	-0,83	0,6889
	3,87	4,70	-0,83	0,6889
	3,88	4,70	-0,82	0,6724
	3,88	4,70	-0,82	0,6724
	3,94	4,70	-0,76	0,5776
	3,99	4,70	-0,71	0,5041
	4,02	4,70	-0,68	0,4624
	4,08	4,70	-0,62	0,3844
	4,08	4,70	-0,62	0,3844
	4,13	4,70	-0,57	0,3249
	4,52	4,70	-0,18	0,0324
	4,53	4,70	-0,17	0,0289
	4,54	4,70	-0,16	0,0256
	4,56	4,70	-0,14	0,0196
	4,60	4,70	-0,10	0,0100
	4,61	4,70	-0,09	0,0081
	4,61	4,70	-0,09	0,0081
	4,62	4,70	-0,08	0,0064
	4,62	4,70	-0,08	0,0064
	4,62	4,70	-0,08	0,0064
	4,68	4,70	-0,02	0,0004
	4,74	4,70	0,04	0,0016
	4,74	4,70	0,04	0,0016
	4,79	4,70	0,09	0,0081
	4,82	4,70	0,12	0,0144
	4,83	4,70	0,13	0,0169
	4,85	4,70	0,15	0,0225
	4,85	4,70	0,15	0,0225
	4,88	4,70	0,18	0,0324
	4,92	4,70	0,22	0,0484
	4,98	4,70	0,28	0,0784
	5,16	4,70	0,46	0,2116
	5,31	4,70	0,61	0,3721
	5,44	4,70	0,74	0,5476
	5,49	4,70	0,79	0,6241
	5,50	4,70	0,80	0,6400
	5,83	4,70	1,13	1,2769
	5,97	4,70	1,27	1,6129
Σ	177,35			11,0447

табл. 1. Расчет абсолютной погрешности ε_i

7. Дисперсия D для характеристики рассеивания:

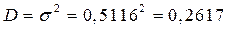
8. Коэффициент вариации K_в для сравнения интенсивности рассеивания:

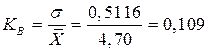
9. Доверительный интервал μ для доверительной вероятности P_g=0.95-0.988:

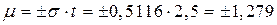
t – аргумент функции Лапласа, t=2,5 - для краткосрочных измерений, проводимых как в полевых условиях, так и в лаборатории.

10. Доверительное действительное (истинное) значение измеряемой величины – контролируемого параметра:

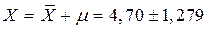
Дата добавления: 2015-05-10