
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теоретические сведения. По дисциплине: Исследование операций
|
|
|
|
ГРАФИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
По дисциплине: Исследование операций
на тему: «Линейное программирование»
Вариант D5
Выполнил студент
группы СУ-02
Паламарчук А. И.
Проверил: Журба В. О.
Сумы 2011 г.
Обязательное домашнее задание по курсу «Исследование
операций»
Решение задачи состоит из двух этапов:
1 этап — построить математическую модель (составить систему ограничений в
виде неравенств и задать целевую функцию);
- решить поставленную задачу графически;
2 этап — на основании составленной системы ограничений (первый этап)
записать систему уравнений в стандартной форме записи ЗЛП;
- составить симплекс - таблицу и решить задачу симплекс - методом;
- сравнить ответы, полученные в этапах 1 и 2.
Вариант D
Завод Electra производит два типа электрических двигателей, каждый на отдельной сборочной линии. Производительность этих линий составляет а1 и а2 двигателей в день. Двигатель первого типа использует в1 единиц некоего комплектующего, а двигатель второго типа в2 единиц этого же комплектующего. Поставщик может обеспечить на день с единиц этого комплектующего. Доходность двигателя первого типа составляет $ d1, второго $ d2. Определите оптимальную структуру ежедневного производства двигателей.
| Вариант | а1 | а2 | в1 | в2 | c | а1 | d2 |
Графический метод решения задачи линейного программирования.
Графический метод, несмотря на свою очевидность и применимость лишь в случае малой размерности задачи, позволяет понять качественные особенности задачи линейного программирования, характерные для любой размерности пространства переменных и лежащие в основе численных методов ее решения. Поясним графический метод на примере задачи ЛП в основной форме для n = 2
(c, x) → max
Ax ≤ b
, где x = (x1, x2), c = (c1, c2), b = (b1, b2,..., bm), A - матрица размера (m × 2).
Очевидно, что при данной постановке задачи допустимое множество X в плоскости (x1, x2) представляет собой многоугольник (не обязательно замкнутый), образованный пересечением полуплоскостей H+aibi (где ai - i-я строка матрицы A, i = 1,..., m), соответствующих ограничениям вида ai1x1 + ai2x2 ≤ bi в исходной задаче. Линии уровня функции f(x) = (c, x) (линией уровня называется множество { }) образуют семейство параллельных прямых Hcα. При этом grad f(x) = c, т.е. градиент целевой функции всюду одинаков и является нормалью каждой из данных полуплоскостей. В соответствии с предыдущим, поиск решения задачи сводится к нахождению максимального числа α* среди всех таких α, что полуплоскость Hcα имеет непустое пересечение с X. При этом - множество решений задачи. При неограниченном решений может и не быть, т.е. при всех.
Из графического представления ясна характерная особенность задачи ЛП (при c ≠ 0): если ее решение существует, то оно достигается обязательно на границе. Отметим, что в рассмотренной задаче ЛП на максимум при поиске α* происходит как бы перемещение прямой Hcα в направлении вектора c. Если же решается задача ЛП на минимум, и, следовательно, ищется минимальное α*, удовлетворяющее указанным требованиям, то Hcα перемещается в направлении, противоположном вектору c.
Выполнение
Целью данной задачи является определить оптимальную структуру ежедневного производства двигателей. Построение математической модели начинаем с идентификации переменных (искомых величин). После этого целевая функция и ограничения выражаются через соответствующие переменные.
Пусть 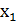 – двигатели первого типа, а
– двигатели первого типа, а 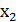 – двигатели второго типа, а z – оптимальное ограничение линии по производству двигателей.
– двигатели второго типа, а z – оптимальное ограничение линии по производству двигателей.
Целевая функция, выражающая структуру ежедневного производства двигателей, будет иметь следующий вид:
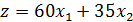
Ограничения, выражающие производительность линии по производству двигателей в день имеют вид:
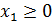 (1)
(1)
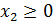 (2)
(2)
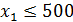 (3)
(3)
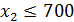 (4)
(4)
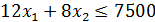 (5)
(5)
Исходя из условий задачи и полученных ограничений, можем построить пространство допустимых решений. По горизонтальной оси отложим Х1, по вертикальной – Х2. Исходя из условия (1,2) можно определить, что все решения находятся в первом квадранте. Построим график и нанесем линии ограничений.
|
|
|
|
|
Дата добавления: 2015-05-10; Просмотров: 982; Нарушение авторских прав?; Мы поможем в написании вашей работы!