Пример 4.2

Изготовлены детали. Одним из наиболее важных параметров каждой из деталей является длина (мм). Проведено 19 измерений этого параметра, результаты приведены в таблице 1.10. Необходимо проверить нормальность распределения случайных погрешностей этого параметра.

Таблица 1.10

Результаты измерений длин деталей

хi, мм	18,035	18,008	18,011	18,009	18,004	18,006
18,010	18,003	18,008	18,006	18,012	18,005
18,007	18,008	18,009	18,008	18,007	18,009	18,010

Решение:

Находим среднее арифметическое значение,

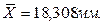
Находим 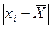для всех 19 значений, для записи промежуточных результатов при расчетах удобнее пользоваться таблицами любой формы.

Затем рассчитывают 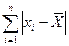. В данном случае эта сумма равна 0,036 мм.

Находим . В данном случае .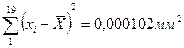

Статистика будет равна

.

Задаем уровень значимости 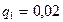. Для нахождения граничных значений статистик используем Приложение 4. Строки n =19 в таблице нет, соседние строки имеют вид

.

Используем линейную интерполяцию

;

.

Условие имеет вид

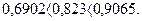
Первый критерий выполняется.

Проверяем второй критерий.

В соответствии с выражением (1.3) =0,028мм. Задаем уровень значимости второго критерия q ₂=0,02.

Используя Приложение 6, находим 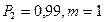, тогда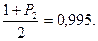

По Приложению 5 находим , учитывая, что .

Далее рассчитываем произведение

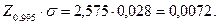
Просматриваем величины разностей 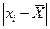и убеждаемся, что ни одна разность не превосходит 0,0072, хотя одно из этих значений могло превзойти 0,0072, так как m =1.

Второй критерий также выполняется. Таким образом, при уровне значимости результаты измерений подчиняются нормальному закону распределения.

Вариант 4.1.

а). При проверке кинокопировального аппарата прерывистой печати методом двукратной экспозиции для кольца кинопленки из 90 кадров получены следующие значения вертикальной неустойчивости в кадровом окне. Проверить нормальность распределения данной погрешности. Результаты измерений (х_i, мм) приведены в таблице 1.11.

Таблица 1.11

Результаты измерений вертикальной неустойчивости

1. Рассчитываем частости по формуле

2.Рассчитывают среднее арифметическое значение 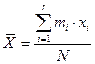(1.1)

3. Вычисляют среднеквадратическое значение (1.3)

4. Далее для расчета критериев согласия по интервалам и суммарного критерия согласия составляют и заполняют табл. 1.9.

r	xi	mi	pi	mi*xi
			0,033333			114,4948
			0,055556			87,26914
			0,044444			40,39309
			0,144444			61,65531
			0,122222			15,25877
			0,122222			0,347654
			0,155556			9,464691
			0,177778			53,1279
			0,033333			23,89481
			0,066667			87,6563
			0,011111			23,25383
			0,022222			67,79654
			0,011111			46,54272
			Xcрa=	8,177778		7,01284
n=			Xcpk=	2,648177
k=

xi-Xcpa	t	p(t)	p(xi)	nPi	xi^2		P1	q
-6,17778	-2,33284	0,0264	0,009969	0,897221	4,928193		0,009969	0,990031
-5,17778	-1,95522	0,0596	0,022506	2,025545			0,022506	0,977494
-4,17778	-1,57761	0,1145	0,043237	3,891357	0,315851		0,043237	0,956763
-3,17778	-1,19999	0,1942	0,073333	6,600013			0,073333	0,926667
-2,17778	-0,82237	0,285	0,107621	9,68591	1,133935		0,107621	0,892379
-1,17778	-0,44475	0,3621	0,136736	12,3062	0,138643		0,136736	0,863264
-0,17778	-0,06713	0,3982	0,150368	13,53309	0,474136		0,150368	0,849632	7,289
0,822222	0,310486	0,3814	0,144024	12,96213	0,083102		0,144024	0,855976
1,822222	0,688104	0,3166	0,119554	10,75986	2,551996		0,119554	0,880446
2,822222	1,065723	0,3939	0,148744	13,38695			0,148744	0,851256
3,822222	1,443341	0,3621	0,136736	12,3062	3,231557		0,136736	0,863264
4,822222	1,820959	0,0761	0,028737	2,586308			0,028737	0,971263
5,822222	2,198578	0,0363	0,013708	1,233679	0,476013		0,013708	0,986292
6,822222	2,576196	0,0147	0,005551	0,499589			0,005551	0,994449	15,086
				Кр.согл.	13,33343

Число степеней свободы в данном случае равно

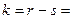14-9=5

Задаем уровень значимости q­­ ₁=0,1 (при уровне надежности Р =0,9). По табл. Приложения 3 находим граничные значения отклонений

;

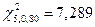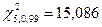
Ответ:

Условие 7,289<13,33<15,086 выполнено, следовательно, распределение можно считать нормальным.

Задача 2.

Проведено 16 измерений шага зуба (х_i , мм) зубчатого барабана. Полученные значения приведены в таблице 1.12. Проверить нормальность распределения данной погрешности.

Таблица 1.12

Результаты измерений шага зуба

4,72	4,71	4,73	4,74	4,70	4,72	4,74	4,73
4,70	4,74	4,71	4,69	4,72	4,70	4,71	4,72

Решение:

1. Находим среднее арифметическое значение ,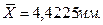

2. Находим 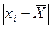для всех 16 значений.

3. рассчитывают 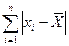. В данном случае эта сумма равна 1,755 мм.

4. Находим 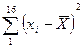. В данном случае .

5. Статистика будет равна

.

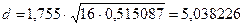6. Задаем уровень значимости 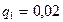. Для нахождения граничных значений статистик используем Приложение 4.

Первый критерий не выполняется

7. Проверяем второй критерий.

Задаем уровень значимости второго критерия q ₂=0,02.

Используя Приложение 6, находим 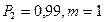, тогда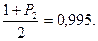

По Приложению 5 находим , учитывая, что .

Далее рассчитываем произведение

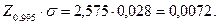
Просматриваем величины разностей 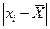и убеждаемся, что все значения больше.

Дата добавления: 2015-05-10