
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Методика и порядок расчета
|
|
|
|
ЦЕЛЬ И ЗАДАЧИ РАБОТЫ
КУРСОВАЯ РАБОТА
РАСЧЕТ ДИНАМИЧЕСКИХ ПАРАМЕТРОВ
РЕЛЬСОВОГО ТРАНСПОРТА ПРИ ПРОХОЖДЕНИИ
КРИВОЛИНЕЙНЫХ УЧАСТКОВ ПУТИ
БЕЗ ПЕРЕХОДНЫХ КРИВЫХ
по дисциплине
ДИНАМИКА ПОДВИЖНОГО СОСТАВА ГЭТ
Выполнил:
Студент гр. 1401, 3 курс
Голин А.
Проверил:
Привалов С.А.
Целью настоящей работы является освоение студентами теоретических методов расчета динамических параметров вагона рельсового транспорта при прохождении им криволинейного участка пути без переходных кривых и обеспечения одинакового силового воздействия вагона на обе рельсовые нити за счет возвышения наружного рельса. В процессе выполнения работы необходимо освоить методику интегрирования дифференциальных уравнений движения численным методом Рунге-Кутта, а также численные методы определения динамических характеристик систем. В указаниях содержатся основные сведения о динамических параметрах рельсового транспорта. Даны примеры расчета параметров вагона.
2.1. Принятые допущения:
- вагон в начальный момент времени имеет скорость V0;
- скорость движения передней тележки вагона (равноускоренное движение)
V1i=V0+ati, (1)
где значения скорости V0 и ускорения движения а берутся из таблицы исходных данных (раздел 5);
- возвышение наружного рельса h рассчитывается в зависимости от координаты Si тележки по формуле:
 - для передней и (2)
- для передней и (2)
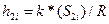 - для задней тележки, (3)
- для задней тележки, (3)
где Lb - расстояние между шкворнями тележек (рис. 1);
R – радиус кривой поворота вагона,
S1i, S2i – путь, пройденный передней и задней тележкой соответственно к моменту времени ti.
Передняя тележка движется по кривой радиуса R, задняя - по прямой.
2.2. Исходные данные:
2.2.1. Геометрические параметры вагона (рис. 1):
- расстояние между шкворнями тележек (база) Lb.
 |
Lb
Рис. 1. Геометрические параметры рельсового вагона
Lb
2.2.2. Параметры пути (рис. 2):
- участок АВ – прямой;
- участок АС имеет радиус R [м]без переходной кривой, т.к. при движении со скоростями меньше 25 км/ч (7 м/с) переходные кривые не предусматриваются [1]. Трамвай на повороте не должен иметь скорость более
V=  [км/ч].
[км/ч].
Все исходные данные для расчета берутся из таблицы (раздел 5).
 C
C
 |
R
 |
A(x1,y1)

B(x2, y2)
 |
Рис. 2. Геометрия криволинейного пути
2.3. Порядок расчета:
1. Вывод уравнений движения вагона по криволинейному рельсовому пути.
2. Интегрирование дифференциальных уравнений движения вагона методом Рунге-Кутта.
3. Определение координат вагона.
4. Расчет значений динамических параметров движения вагона.
5. Построение графиков зависимости динамических характеристик движения вагона.
6. Заключение о выборе скоростного режима вагона по криволинейному участку пути.
2.4. Вывод уравнений движения вагона по криволинейному рельсовому пути.
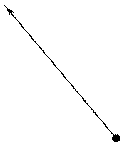
Согласно заданным исходным условиям скорость движения передней тележки определяется как
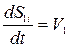 (ti). (4)
(ti). (4)
При движении по кругу радиуса R на криволинейном участке путь, пройденный передней тележкой, можно найти по формуле
S1i=R*ai, (5)
где a i - центральный угол кривой поворота передней тележки (рис. 3), откуда, учитывая, что R=const, можно получить в каждый момент времени
 . (6)
. (6)
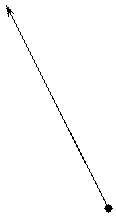
Из уравнения (4) следует
 . (7)
. (7)
 |
 x
x
 g
g
R


 A(x1, y1)
A(x1, y1)
 B(x2, y2)
B(x2, y2)



b
a
 |
y
Рис. 3. Угловые параметры движения вагона
2.5. Интегрирование дифференциальных уравнений движения вагона методом Рунге-Кутта.
2.5.1. Выбор шага интегрирования. Начальный шаг интегрирования выбирается из условия
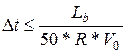 . (8)
. (8)
Значение шага округляется и принимается не более первой значащей цифры.
2.5.2. Интегрирование уравнения движения [2, 3].
ti=t0+i*Dt; (9)
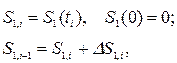 (10)
(10)
где
 (11)
(11)
Расчет коэффициентов в формуле (11) производится на каждом шаге интегрирования по формулам [2]:
 (12)
(12)
Для проверки правильности выбора шага необходимо после окончания расчета с выбранным шагом выполнить весь расчет с новым шагом Dt1=Dt/2.
Если расхождение полученных значений угла a не превышает допустимой погрешности dк=|a(Dt1)-a(Dt)|<0,01, то шаг выбран правильно. В противном случае шаг уменьшается в два раза и вновь выполняется расчет с новым шагом Dt2=Dt1/2. Так до тех пор, пока не будет достигнута заданная погрешность.
2.6. Определение координат вагона.
Угол, на который повернулась передняя тележка за время от t0 до ti, может быть найден по формуле (6)

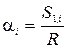 .
.
Тогда координаты передней тележки в момент времени ti будут равны
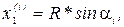
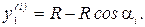 (13)
(13)
Координаты задней тележки в этот момент времени определяются формулами
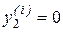 , (14)
, (14)
когда задняя тележка движется строго по прямой вдоль оси Х, и
 (15)
(15)
при движении по криволинейному участку.
Координаты задней тележки по оси х могут быть найдены по формулам
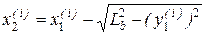 (16)
(16)
при движении по прямолинейному участку и
 (17)
(17)
- по криволинейному участку.
Здесь и далее b - центральный угол вагона, определяемый из условия (рис.3),
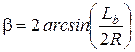 . (18)
. (18)
Угол поворота вагона в момент времени ti (рис. 3)
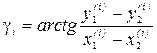 . (19)
. (19)
2.7. Расчет значений динамических параметров движения вагона.
Одним из основных динамических параметров является ускорение. Причем при криволинейном движении значение ускорения в различных точках вагона различно, особенно в переходный период от прямолинейного движения к криволинейному.
Для представления всей картины изменения ускорения в различных точках вагона необходимо определить значения ускорений как минимум в двух точках, например, в местах крепления тележек.
Точка 1 вагона с координатами (x1, y1) движется строго по окружности радиуса R и имеет касательное ускорение, равное а, и центробежное (нормальное)
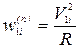 . (20)
. (20)
Кроме того, при возвышении наружного рельса в точке 1 действует ускорение в горизонтальной плоскости, равное проекции ускорения свободного падения (рис. 4)
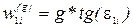 , (21)
, (21)
где
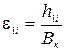 (22)
(22)
угол крена вагона в точке 1, Вк – ширина колеи.
 |

 wi(g)
wi(g)
 | |||
 | |||

 ei
ei


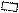
 g
g
 hi eI
hi eI


 Вк
Вк
 |
Рис. 4. Возвышение наружного рельса
Возвышение наружного рельса зависит от координаты Si, изменяясь от нуля в точке с х=-Lb до максимального значения при a=p/4, и определяется по формуле
hji=k(Sji+Lb)/R (23)
для каждой j -й тележки, где k= 0,152 учитывает смещение центра тяжести экипажа в наружную сторону от оси кривой.
При этом координата S2i=x2i - Lb.
Результирующим значением будет геометрическая сумма этих ускорений, т.е.
 . (24)
. (24)
В точке 2 доля ускорения а, действующая на вагон, направлена строго по оси х. Поэтому

Так как движение вагона может быть представлено как прямолинейное движение точки крепления задней тележки и вращение всего вагона вокруг этой точки, то проекция значения ускорения а в точке 2 равна
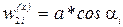 . (25)
. (25)
При возвышении наружного рельса в точке 2 действует ускорение в горизонтальной плоскости, равное проекции ускорения свободного падения
 , (26)
, (26)
где
 (27)
(27)
угол крена вагона в точке 2.
Результирующим значением будет геометрическая сумма этих ускорений, т.е.
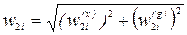 . (28)
. (28)
Значения ускорений в других точках вагона могут быть определены как сумма ускорения, действующего вдоль оси х в точке 2 вагона, и ускорения, вызванного вращением вагона вокруг точки 2.
2.8. Построение графиков зависимости динамических характеристик движения вагона.
Для наглядного представления динамических параметров, характеризующих движение вагона на переходном участке, необходимо построить графики зависимости:
- V1(t), V2(t) – изменение значения скорости движения передней и задней тележек соответственно от времени (рис. 1 Приложения 2);
- a(t), g(t) – изменение угла поворота передней тележки и вагона от времени (рис. 2 Приложения 2);
- w1(t) – ускорение движения передней тележки с учетом и без учета возвышения наружного рельса (рис. 3 Приложения 2);
- w2(t) – ускорение движения задней тележки вагона с учетом и без учета возвышения наружного рельса (рис. 4 Приложения 2).
2.9. Заключение.
В заключении приводятся:
- значение величины выбранного шага интегрирования с указанием полученной погрешности dк;
- пределы интегрирования с обоснованием выбора их значений;
- описание изменений линейных и угловых координат вагона;
- анализ изменений динамических параметров вагона.
При анализе изменений динамических параметров вагона необходимо использовать графические материалы.
В заключении дается анализ возможности использования заданного режима движения вагона при переходе на криволинейный участок пути и указываются направления улучшения динамических характеристик с целью уменьшения действующих на пассажиров нагрузок.
|
|
|
|
|
Дата добавления: 2015-05-10; Просмотров: 304; Нарушение авторских прав?; Мы поможем в написании вашей работы!