Решение задач Штурма-Лиувилля

Задачу Штурма-Лиувилля в общем виде мы, конечно, решить не сможем. Однако некоторые частные случаи удается разобрать до конца и получить формулы для собственных значений и собственных функций. Разберем эти случаи.

Вначале рассмотрим уравнение (18) y'' + λy = 0. и краевые условия первого рода (19) y(a) = y(b) = 0. Для удобства будем считать, что a = 0 и b = l > 0. К такой задаче можно всегда свести данную задачу, если сделать замену переменной x' = x - a, при этом вид уравнения не изменится.

Вид общего решения уравнения (18) зависит от значений параметра λ. Разберем три случая: 1) λ < 0, 2) λ = 0, 3) λ > 0. В первом случае обозначим λ = - k². Тогда характеристическое уравнение r² - k² = 0 будет иметь действительные различные корни r₁ = k, r₂ = - k: Поэтому, общее решение дифференциального уравнения запишется в виде y = C₁e^kx + C₂e^-kx. Подставим краевые условия в общее решение и получим

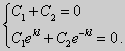
Определитель этой системы равен

Следовательно, система имеет только нулевое (тривиальное) решение C₁ = C₂ = 0. Значит, при λ < 0 данная задача не имеет собственных значений. Если λ = 0, то общее решение уравнения y'' = 0 записывается в виде y = C₁x + C₂. При подстановке краевых условий получим: 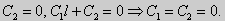Поэтому, точка λ = 0 также не является собственным значением задачи. Наконец, в третьем случае обозначим λ = k² и получим характеристическое уравнение r² + k² = 0. Оно имеет комплексные корни r₁ = ki и r₂ = -ki и общее решение дифференциального уравнения в этом случае запишется в виде y = C₁cos kx + C₂sin kx. Подставим краевые условия в общее решение:

(22)

Для того, чтобы эта система имела нетривиальные решения, необходимо и достаточно, чтобы sin kl = 0. Следовательно kl = πn, то есть 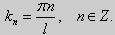Так как 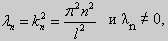то можно ограничиться только положительными значениями n = 1, 2,.... Таким образом, собственные значения данной задачи имеют вид 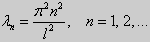При этих значениях алгебраическая система (22) имеет решения:C₁ = 0, C₂ - любое действительное число. Подставим эти значения в общее решение дифференциального уравнения и получим собственные функции задачи

Обычно постоянный множитель выбирают либо равным единице, либо из условия нормировки:

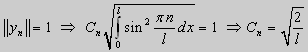
По тому же алгоритму решаются задачи Штурма-Лиувилля следующего вида:

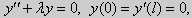
(23)

и

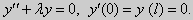
(24)

Эти задачи так же, как и предыдущая, при λ 0 не имеют собственных значений. В случае λ > 0 общее решение уравнения записывается в виде y = C₁cos kx +C₂sin kx, где После подстановки у в краевые условия, получим:

а) для задачи (23)

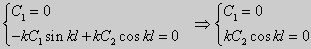
b)для задачи (24)

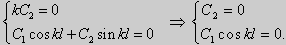
Для того, чтобы эти системы уравнений имели нетривиальные решения, необходимо и достаточно, чтобы cos kl = 0. Следовательно, 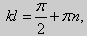то есть 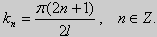Отрицательные значения n можно не рассматривать, так как 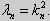Таким образом, собственные значения у этих задач одинаковые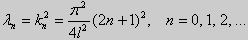

Собственные функции задачи (23) имеют вид А у задачи (24) они другие:

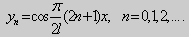
Некоторые отличия возникают при решении задачи Штурма-Лиувилля в случае краевых условий второго рода

y'' + λy = 0, y'(0) = y'(l) = 0.

(25)

Рассуждениями, аналогичными тем, которые проводились для краевых условий первого рода, можно показать, что задача (25) при λ < 0 не имеет собственных значений. А вот λ = 0 является собственным числом. В самом деле, при λ = 0 общее решение уравнения имеет вид y = C₁x + C₂. После подстановки у в краевые условия (25) получим: C₁ = 0, C₂ - любое действительное число. Следовательно, функция у = 1 является собственной функцией задачи. Другие собственные значения и собственные функции получаются при λ > 0. В этом случае, общее решение уравнения имеет вид y = C₁cos kx + C₂sin kx, 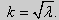Найдем производную этой функции и подставим в нее краевые условия (25):

Эта алгебраическая система имеет нетривиальные решения тогда и только тогда, когда, sin kl = 0 то есть kl = πn или 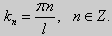Таким образом, числа 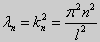также являются собственными значениями задачи. Собственные функции при этих значениях имеют вид . Окончательно, задача (25) имеет собственные значения и собственные функции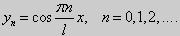

Для задачи Штурма-Лиувилля с краевыми условиями третьего рода (21) уже не удается получить собственные значения в явном виде. В качестве примера рассмотрим одну такую задачу, когда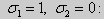

y'' + λy = 0, y'(0) = y(0), y'(l) = 0.

(26)

При 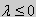задача (26) не имеет собственных значений и собственных функций. Доказательство этого проводится так же, как и для краевых условий первого рода. При λ > 0 общее решение уравнения записывается в виде y = C₁cos kx + C₂sin kx, где 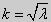. После дифференцирования этой функции и подстановки её производной и самой функции в краевые условия (26) будем иметь:

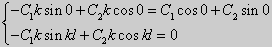
или

(27)

Получившаяся алгебраическая система будет иметь нетривиальные решения только в том случае, когда

cos kl - ksin kl = 0

или

ctg kl = k

(28)

Уравнение (28) является трансцендентным уравнением относительно k. Оно не решается в явном виде. Однако, построив графики левой и правой частей уравнения (28), видно, что оно имеет бесконечно много решений (см. рис.13). Обозначим корни уравнения (28) через r_n, n = 1,2,.... Тогда при

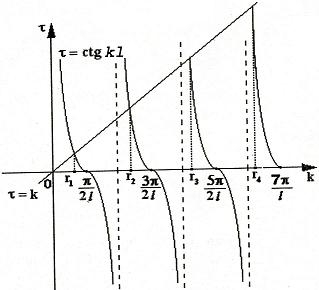
Рис.13

Численными методами можно найти приближенные значения r_n. Из системы (27) при k = r_n получим C_1n = r_nC_2n, где C_2n -произвольные постоянные. При этих значениях постоянных решения дифференциального уравнения будут иметь вид

y_n = C_2n (r_n cos r_nx + sin r_nx).

Они являются собственными функциями краевой задачи (26) с собственными значениями

Дата добавления: 2015-05-10