
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Удар абсолютно упругих и неупругих тел
|
|
|
|
Удар абсолютно упругих и неупругих тел является примером применения законов сохранения импульса и энергии при решении физической задачи.
Удар (или соударение) - это столкновение двух или более тел, взаимодействующих очень короткое время. Кроме ударов в прямом смысле этого слова (столкновения атомов или игровых шаров) сюда можно отнести и такие, как столкновение человека с землей при прыжке с парашюта и пр. Силы взаимодействия между сталкивающимися телами столь велики, что мы можем пренебречь прочими внешними силами, действующими на них. Это позволяет приближенно рассматривать систему тел в процессе их соударения как замкнутую и применять к ней законы сохранения.
При ударе тела испытывают деформацию. Понятие удара подрузамевает, что кинетическая энергия относительного движения ударяющихся тел на короткое время преобразуется в энергию упругой деформации. Во время удара имеет место перераспределение энергии между соударяющимися телами. Опыты показывают, что относительная скорость тел после соударения не достигает своего значения до соударения. Это объясняется тем, что не бывает идеально упругих тел и идеально гладких поверхностей. Отношение нормальной составляющей относительной скорости тел после удара к нормальной составляющей относительной скорости тел до удара называется коэффициентом восстановления ε: ε = νn'/νn
Если для соударяющихся тел ε=0, то такие тела называются абсолютно неупругими, если ε=1 - абсолютно упругими. На практике для всех тел 0<ε<1 (например, для шаров из слоновой кости ε=0,89; для стальных шаров ε=0,56, для свинца ε≈0). Но в некоторых случаях тела можно с большой степенью точности рассматривать либо как абсолютно неупругие, либо как абсолютно упругие.
Линией удара называется прямая, проходящая через точку соприкосновения тел и перпендикулярная к поверхности их соприкосновения. Удар называется центральным, если соударяющиеся тела до удара движутся вдоль прямой, проходящей через центры их масс. Здесь мы рассматриваем только центральные абсолютно упругие и абсолютно неупругие удары.
Абсолютно упругий удар - соударение двух тел, в результате которого в обоих участвующих в столкновении телах не остается никаких деформаций и вся кинетическая энергия тел до удара после удара снова превращается в первоначальную кинетическую энергию (отметим, что это идеализированный случай).
Для абсолютно упругого удара выполняются закон сохранения кинетической энергии и закон сохранения импульса.
Обозначим скорости шаров массами m1 и m2 до удара через ν1 и ν2, после удара - через ν1' и ν2' (рис. 1). Для прямого центрального удара векторы скоростей шаров до и после удара лежат на прямой линии, проходящей через их центры. Проекции векторов скоростей на эту линию равны модулям скоростей. Их направления учтем знаками: положительное соотнесем движению вправо, отрицательное - движению влево.
При указанных допущениях законы сохранения имеют вид
(1) 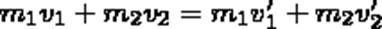
(2) 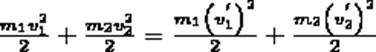
Произведя соответствующие преобразования в выражениях (1) и (2), получим
(3) 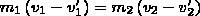
(4) 
откуда
(5) 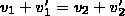
Решая уравнения (3) и (5), находим
(6
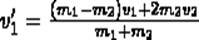
(7) 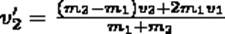
Разберем несколько примеров.
1. При ν2=0
(8) 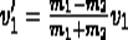
(9) 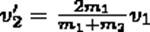
Проанализируем выражения (8) в (9) для двух шаров различных масс:
а) m1=m2. Если второй шар до удара висел неподвижно (ν2=0) (рис. 2), то после удара остановится первый шар (ν1'=0), а второй будет двигаться с той же скоростью и в том же направлении, в котором двигался первый шар до удара (ν2'=ν1);
б) m1>m2. Первый шар продолжает двигаться в том же направлении, как и до удара, но с меньшей скоростью (ν1'<ν1). Скорость второго шара после удара больше, чем скорость первого после удара (ν2'>ν1')
в) m1<m2. При ударе направление движения первого шара изменяется - шар отскакивает обратно. При этом второй шар движется в сторону, в которую двигался первый шар до удара, но с меньшей скоростью, т. е. ν2'<ν1
г) m2>>m1 (например, столкновение шара со стеной). Из уравнений (8) и (9) следует, что ν1'= -ν1; ν2' ≈ 2m1ν2'/m2.
2. При m1=m2 выражения (6) и (7) будут иметь вид ν1'= ν2; ν2'= ν1; т. е. шары равной массы как бы обмениваются скоростями.
Абсолютно неупругий удар - соударение двух тел, в результате которого тела соединяются, двигаясь дальше как единое целое. Абсолютно неупругий удар можно продемонстрировать с помощью шаров из пластилина (глины), которые движутся навстречу друг другу.
Если массы шаров m1 и m2, их скорости до удара ν1 и ν2, то, используя закон сохранения импульса

где v - скорость движения шаров после удара. Тогда 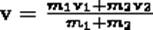
В случае движения шаров навстречу друг другу они вместе будут продолжать движение в ту сторону, в которую двигался шар с большим импульсом. В частном случае, если массы шаров равны (m1=m2), то 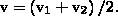
Определим, как изменяется кинетическая энергия шаров при центральном абсолютно неупругом ударе. Так как в процессе соударения шаров между ними действуют силы, зависящие от их скоростей, а не от самих деформаций, то мы имеем дело с дисипативными силами, подобным силам трения, поэтому закон сохранения механической энергии в этом случае не должен соблюдаться. Вследствие деформации происходит уменьшение кинетической энергии, которая переходит в тепловую или другие формы энергии. Это уменьшение можно определить по разности кинетической энергии тел до и после удара: 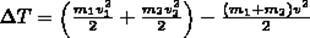
Используя (10), получаем 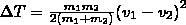
Если ударяемое тело было первоначально неподвижно (ν2=0), то 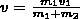
и 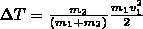
Когда m2>>m1 (масса неподвижного тела очень велика), то ν<<ν1 и практически вся кинетическая энергия тела переходит при ударе в другие формы энергии. Поэтому, например, для получения значительной деформации наковальня должна быть значительно массивнее молота. Наоборот, при забивании гвоздей в стену масса молота должна быть гораздо большей (m1>>m2), тогда ν≈ν1 и почти вся энергия тратится на возможно большее перемещение гвоздя, а не на остаточную деформацию стены.
Абсолютно неупругий удар - это пример потери механической энергии под действием диссипативных сил.
|
|
|
|
|
Дата добавления: 2015-05-10; Просмотров: 840; Нарушение авторских прав?; Мы поможем в написании вашей работы!