
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Розв’язання. Завдання 1.Розв’язати нелінійне рівняння 3x4+4х3=12х2+π методом половинного ділення і комбінованим методом на інтервалі хϵ[-20;20] з похибками
|
|
|
|
Варіант 9
Завдання 1.Розв’язати нелінійне рівняння 3x4+4х3=12х2+π методом половинного ділення і комбінованим методом на інтервалі хϵ[-20;20] з похибками 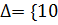 -3,10-4,10-5}.
-3,10-4,10-5}.
Зводимо рівняння до вигляду 3x4+4х3-12х2-π =0 і табулюємо функцію
f(x)=3x4+4х3-12х2-π.
Програма табулювання в Сі
#include<conio.h>
#include<math.h>
#include<stdio.h>
float f(float x)
{return 3*pow(x,4)+4*pow(x,3)-12*pow(x,2)-M_PI;
}
main()
{float x; clrscr();
for(x=-20;x<=20;x+=4)
printf(“\n x=%4.1f f(x)=%5.2f”,x,f(x)); return 0;
}
Peзультати табулювання в Сі
| x | -20 | -16 | -12 | -8 | -4 | ||||||
| f(x) | -3.14 |
Із таблиці зрозуміло,що функція на цьому інтервалі двічі змінює знак,а значить рівняння має два корені. Вибираємо інтервал хϵ[-4;4]
Програма табулювання функції і побудови її графіка у MatLab на інтервалі хϵ[-20;0].
clc;clear;
a=-4;b=4;
x=[a:(b-a)/10:b];
y=f_lva9(x);
disp('x y');disp([x' y']);
figure(1);
plot(x,y,x,y,'*');grid;
xlabel('x'); ylabel('f(x)');
Файл-функція f_lva9.m
function [y]=f_lva9(x);
y=3*x.^4+4*x.^3-12*x.^2-pi;
Результати табулювання в MatLab
| x | -4 | -3.2 | -2.4 | -1.6 | -0.8 | 0 | 0.8 | 1.6 | 2.4 | 3.2 | 4 |
| f(x) | 316.8 | 57.4 | -28 | -30.6 | -11.6 | -3.14 | -7.5 | 2.2 | 82.5 | 319.6 | 828.8 |
хϵ[-2.8076;-2.8026];
Тепер уточнюємо значення кореня заданими числовими метод
Метод половинного ділення
Блок-схема функції
| Початок |
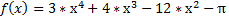
|
| Кінець |
Блок-схема основного алгоритму
| Початок |
Ввід a, b, 
|
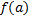
|
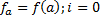
|
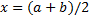
|

|
Ні Так
Вивід 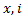
|
| Кінець |
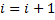
|
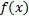
|

|
Так Ні
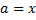
|
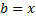
|
Програма (файл mpd1_lva9.cpp) визначення кореня методом ПД в Сі
#include<conio.h>
#include<math.h>
#include<stdio.h>
float f(float x)
{return 3*pow(x,4)+4*pow(x,3)-12*pow(x,2)-M_PI; }
main()
{int i=0;float x,fa,,a=-20,b=20,Delta;
clrscr();puts(“\n Input a”);scanf(“%f”,&a);puts(“\n Input b”);scanf(“%f”,&b);
fa=f(a);
A: x=(a+b)/2;
If((b-a)<Delta)
printf(“\n x=%.f i=%.d”,x,i);
else {if(fa*f(x)>0) a=x;
else b=x;
i++;goto A;}
return 0;}
Розв ’ язки рівняння методом половинного ділення в Сі
| Задана абсолютна похибка | 
| 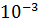
| 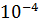
| 
|
| Виведене значення кореня | 
| -2.806091 | -2.806129 | -2.806163 |
| Наближене значення кореня | 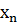
| -2.805±0.001 | 2.8060±0.0001 | -2.80615±0.00001 |
| Кількість ітерацій | n | 16 | 19 | 22 |
Програма (файл mpd1_lva9.m) визначення кореня методом ПД в MatLab
clc;clear; a=input('a '); b=input('b ');Delta=input('Delta ');
i=0;fa=f_lva9(a);x=(a+b)/2;while (b-a)>Delta
if fa*f_lva9(x)>0 a=x;
else b=x;
end;
x=(a+b)/2; i=i+1;end;
format long;disp('x i');disp([x i])
Розв ’ язки рівняння методом половинного ділення в MatLab
| Задана абсолютна похибка | 
| 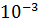
| 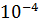
| 
|
| Виведене значення кореня | 
| -2.806091 | -2.806129 | -2.806163 |
| Наближене значення кореня | 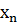
| -2.805±0.001 | -2.8060±0.0001 | -2.80615±0.00001 |
| Кількість ітерацій | n | 16 | 19 | 22 |
Комбінований метод (хорд і дотичних)
Перша похідна заданої функції: f’(x)=12 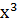 +12
+12 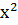 -24x.
-24x.
Блок-схема функції f(x) Блок-схема функція f’(x)
| Початок |
| Початок |
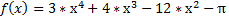
|
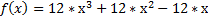
|
| Кінець |
| Кінець |
Блок-схема основного алгоритму
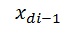 =b =b
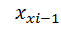 =a =a
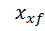 =b =b
|
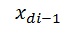 =a =a
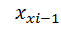 =b =b
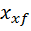 =a =a
|
| f(a)*f(c)>0 |

|
| Початок |
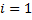
|
Ввід a, b, 
|
| c=a-(b-a)*f(a)/(f(b)-f(a)) |

|
Ні Так
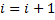
|
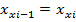
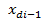 = = 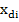
 = = 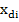
|
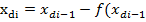 )/f’ )/f’  ) )
|
f’( 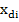 ) )
|
f(x); x={  ; ; 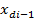 ; ;  } }
|
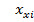 = =  -( -(  - -  )*f( )*f(  )/f’( )/f’(  )) ))
|
 - - 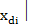 < <    
|
Ні
Так
Вивід (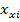 + + 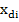 )/2,i )/2,i
|
| Кінець |
Програма (файл mk1_lva9.cpp) визначення кореня комбінованим методом в Сі
#include<stdio.h>
#include<conio.h>
#include<math.h>
float f(float x) {return 3*pow(x,4)+4*pow(x,3)-12*pow(x,2)-M_PI;}
float f1(float x) {return 12*pow(x,3)+12*pow(x,2)-24*x;}
main()
{int i=1;
float xxi,xxi1,xdi,xdi1,xxf,a=-20,b=20,c,Delta;
clrscr();
puts("\n Input a"); scanf("%f",&a); puts("\n Input b"); scanf("%f",&b);
puts("\n Input Delta"); scanf("%f",&Delta);
c=a-(b-a)*f(a)/(f(b)-f(a));
if(f(a)*f(c)>0) {xdi1=b;xxi1=a;xxf=b;}
else {xdi1=a;xxi1=b;xxf=a;}
xxi=xxi1;xdi=xdi1;
while(fabs(xxi-xdi)>Delta)
{xxi=xxi1-(xxi1-xxf)*f(xxi1)/(f(xxi1)-f(xxf)); xdi=xdi1-f(xdi1)/f1(xdi1);
xdi1=xdi;xxi1-xxi;xxf=xdi;i++; printf("\n x=%f i=%d",(xxi+xdi)/2.0,i);
}
return 0;
}
Розв ’ язки рівняння комбінованим методом в Сі
| Задана абсолютна похибка | 
| 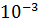
| 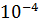
| 
|
| Виведене значення кореня | 
| 1.543340 | 1.543340 | 1.543333 |
| Наближене значення кореня | 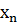
| 1.544±0.001 | 1.5434±0.0001 | 1.54334±0.00001 |
| Кількість ітерацій | n | 14 | 14 | 15 |
Програма(файл mk1_lva9.m) визначення кореня комбінованим в MatLab
clc;clear; a=input('a');b=input('b');Delta=input('Delta'); i=1;
c=a-(b-a)*f_lva9(a)/(f_lva9(b)-f_lva9(a));
if f_lva9(a)*f_lva9(c)>0, xdi1=b;xxi1=a;xxf=b;
else xdi1=a;xxi1=b;xxf=a;
end
xxi=xxi1; xdi=xdi1;
while abs(xxi-xdi)>Delta
xxi=xxi1-(xxi1-xxf)*f_lva9(xxi1)/(f_lva9(xxi1)-f_lva9(xxf));
xdi=xdi1-f_lva9(xdi1)/f1_lva9(xdi1);
xdi1=xdi;xxi1=xxi;xxf=xdi;i=i+1;
end;
format long; disp('x i'); disp([(xxi+xdi)/2 i]);
Файл-функція f1_lva9.m, в якій записана перша похідна f(x).
function [ y ] = f1_lva9(x);
y=12*x.^3+12*x.^2-12*x;
Розв ’ язки рівняння комбінованим методом в MatLab
| Задана абсолютна похибка | 
| 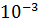
| 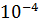
| 
|
| Виведене значення кореня | 
| 1.543520 | 1.543354 | 1.543335 |
| Наближене значення кореня | 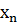
| 1.544±0.001 | 1.5434±0.0001 | 1.54334±0.00001 |
| Кількість ітерацій | n | 17 | 19 | 21 |
Порівняльна таблиця результатів обчислень різними методами
| Метод уточнення кореня | Задана абсолютна похибка, 
| Значення кореня | Кількість ітерацій | ||
| Сі | MatLab | Сі | MatLab | ||
| Половинного ділення | 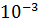
| -2.806091 | -2.806091 | ||
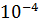
| -2.806129 | -2.806129 | |||

| -2.806163 | -2.806163 | |||
| Комбінований | 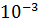
| 1.543340 | 1.543520 | ||
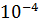
| 1.543340 | 1.543354 | |||

| 1.543333 | 1.543335 |
Роз’язок рівняння в Matlab за допомогою функції fzero().Якщо файл tab1_lva9.m
Доповнити цією функцією,то отримаємо розв’язок рівняння: -2.806159. Ця команда,
Наприклад,має вигляд: y_zero=fzero(‘f_lva9’,(a+b)/2).
|
|
|
|
Дата добавления: 2015-05-10; Просмотров: 421; Нарушение авторских прав?; Мы поможем в написании вашей работы!