Эллипсоид

Классификация поверхностей второго порядка.

Общее уравнение поверхности второго порядка

Реферат

Тема	Поверхности второго порядка
Студента	Руденко Павла Владимировича
(Фамилия, имя, отчество)
Преподаватель	Лукша В.В.
(Ф.И.О.)

Оценка
Дата
Подпись

Волгоград

Оглавление

1. Общее уравнение поверхности второго порядка. 3

2. Классификация поверхностей второго порядка. 3

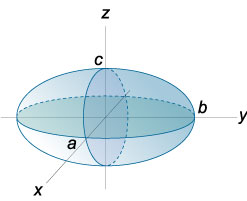
3. Эллипсоид. 4

4. Мнимый эллипсоид. 4

5. Однополостный гиперболоид. 5

6. Двуполостный гиперболоид. 5

7. Коническая поверхность. 6

8. Мнимая коническая поверхность. 6

9. Эллиптический параболоид. 6

10. Гиперболический параболоид. 7

11. Эллиптический цилиндр. 7

12. Мнимый эллиптический цилиндр. 8

13. Гиперболический цилиндр. 8

14. Пересекающиесяплоскости. 8

15. Мнимыепересекающиесяплоскости. 8

16. Параболическийцилиндр. 9

17. Параллельныеплоскости. 9

18. Мнимыепараллельныеплоскости. 9

19. Совпадающиеплоскости. 9

20. Уравнение сферы с центром в начале координат. 9

21. Уравнение сферы с центром в произвольной точке. 10

22. Уравнение сферы по заданным концам диаметра. 10

23. Уравнение сферы по четырем точкам. 10

24. Общее уравнение сферы. 10

Ax²+By²+Cz²+ 2Fyz+ 2Gzx+ 2Hxy+ 2Px+ 2Qy+ 2Rz+D= 0,где x, y, z− координаты точек поверхности,A,B,C,... − действительные числа.

Данная классификация основана на рассмотрении инвариантов поверхностей второго порядка. Инварианты представляют собой специальные выражения, составленные из коэффициентов общего уравнения, которые не меняются при параллельном переносе или повороте системы координат. Всего можно выделить 17 различных канонических видов поверхностей.

#	Ранг (e)	Ранг (E)	Δ	Знаки k	Вид поверхности
			< 0	Одинаковые	Эллипсоид
			> 0	Одинаковые	Мнимый эллипсоид
			> 0	Разные	Однополостный гиперболоид
			< 0	Разные	Двуполостный гиперболоид
				Разные	Коническая поверхность
				Одинаковые	Мнимая коническая поверхность
			< 0	Одинаковые	Эллиптический параболоид
			> 0	Разные	Гиперболический параболоид
				Одинаковые	Эллиптический цилиндр
				Одинаковые	Мнимый эллиптический цилиндр
				Разные	Гиперболический цилиндр
				Разные	Пересекающиеся плоскости
				Одинаковые	Мнимые пересекающиеся плоскости
					Параболический цилиндр
					Параллельные плоскости
					Мнимые параллельные плоскости
					Совпадающие плоскости

В качестве инвариантов используются ранги матриц e и E, определитель матрицы E и знаки корней характеристического уравнения для матрицы e. Указанные матрицы имеют вид:

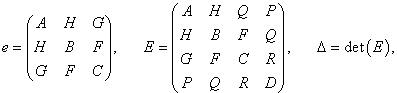
а корни k ₁, k ₂, k ₃ находятся из решения уравнения

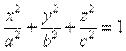
4. Мнимый эллипсоид.

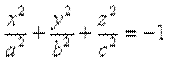
Дата добавления: 2015-05-10