Методические указания. Т а б л и ц а 5 № вариан- - та Исходные данные 1 группы Исходные данные 2 группы Исходные данные 3 группы Нагрузка

Т а б л и ц а 5

№ вариан- - та	Исходные данные 1 группы	Исходные данные 2 группы	Исходные данные 3 группы
Нагрузка подстанций	cosj	Длина участка сети, км	Длина участка сети, км
S1, МВА	S2, МВА	S3, МВА	S4, МВА	А-1	1-2	2-3	3-4	2-4	В-4
I					0,85
II					0,88
III					0,9
IV					0,86
V					0,91
VI					0,85
VII					0,89
VIII					0,92
IX					0,84
X					0,87

В ряде случаев при проектировании, а также при эксплуатации сетей небольшой сложности возникает необходимость проведения одноразовых расчетов без применения ПЭВМ, одним из распространенных способов ручного счета – последовательное упрощение схемы сложной сети по методу преобразования сети.

Сущность метода преобразования заключается в том, что заданную сложную сеть путем постепенных преобразований приводят к линии с двусторонним питанием, в которой распределение мощностей находят уже известным методом. Затем, после определения линейных мощностей на каждом участке преобразованной схемы, с помощью последовательных обратных преобразований находят действительное распределение мощностей в исходной схеме сети.

Эквивалентирование параллельных линии на любых участках замкнутой сети возможно только в том случае, если на этих линиях нет присоединенных нагрузок. Для участка замкнутой сети с двумя параллельными линиями (см.рисунок 2.2)

= + ; .

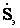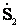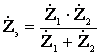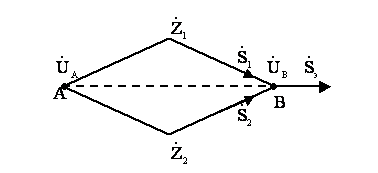
Рисунок 2.2

Если в схеме существуют промежуточные нагрузки, то эквивалентирование осуществить нельзя. Для этого делают так называемый перенос нагрузок в другие точки сети. При этом режим сети до переноса и после должен оставаться неизменным.

Иногда при расчете сети требуется произвести преобразования треугольника в эквивалентную звезду и обратно (см.рисунок 2.3).

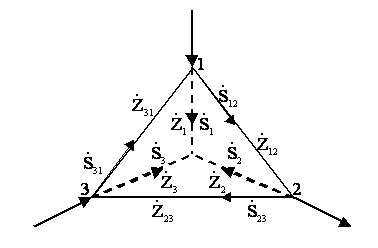
Рисунок 2.3

Сопротивления лучей эквивалентной звезды определяются

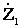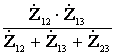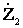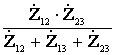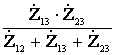= ; = ; = . (2.1)

Обратные преобразования

(2.2)

При развертывании преобразований схемы в исходную необходимо найти распределение мощностей на сторонах треугольника по полученному распределению мощностей в лучах эквивалентной звезды.

После предварительного определения мощностей выбирается сечение проводов и проводится уточненный расчет мощностей с учетом действительных сопротивлений каждого участка сети.

Расчет напряжений осуществляется по «данным начала». В этом случае известной величиной является напряжение в центрах питания _А и U_В и используется метод последовательных приближений, причем расчеты выполняются в два этапа.

В качестве первого приближения (на первом этапе расчета) принимается, что напряжения во всех узлах равны номинальному напряжению сети. При этом условии находится распределение мощностей в сети.

Расчет ведется в следующей последовательности. Определяются потери мощности на концевом участке сети

DP = ,

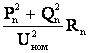(2.3)

DQ = .

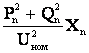Далее определяется мощность 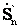в начале этого участка. По балансу мощности в узле (n-1) определяется мощность в конце участка n-1. Аналогично ведется расчет и для всех остальных участков сети. Расчет продолжается до тех пор, пока не определится .

На следующем этапе расчета определяются напряжения в узлах нагрузки во втором приближении. Исходными данными для расчета являются: напряжение 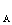и найденные в предыдущем этапе расчета мощности в конце каждого из участков. Для головного участка сети

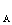= - D , (2.4)

где D - падение напряжения на головном участке сети.

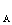= - DU - jdU (2.5)

или в раскрытой форме

= U 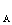- - 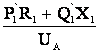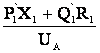. (2.6)

Модуль напряжения в точке 1

U = 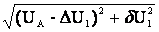. (2.7)

Аналогично определяются напряжения в других узловых точках сети.

Дата добавления: 2015-05-10