Физическая и химическая адсорбция

Поверхностные явления

Термодинамическая система, состоящая из двух и более фаз, называется гетерогенной. В гетерогенной системе фазы отделены друг от друга поверхностями раздела. Вблизи поверхности физико-химические свойства фазы отличаются от свойств в объёме фазы. Так энергия молекул на поверхности отличается от энергии молекул в глубине фазы. Это связано с тем, что связи молекул, находящихся в поверхностном слое ненасыщенны. Характер движения молекул на поверхности будет иным, чем в середине твёрдого тела. Вследствие этого концентрация растворённого вещества на поверхности фазы будет отличаться от концентрации растворённого вещества в глубине фазы. Такое явление получило название поверхностного сгущения компонента. Поверхностное сгущение компонента,

приходящиеся на единицу площади поверхности фазы, называется адсорбцией:

n = Г (3.1)

где n - поверхностное сгущение i – го компонента на k – ой

поверхности;

Г - адсорбция i – го вещества на k – ой поверхности.

Процесс, противоположный процессу адсорбции, называется десорбцией. Вещество, которое адсорбируется на поверхности фазы, называется адсорбатом или адсорбтивом. Вещество, на поверхности которого осуществляется адсорбция, называется адсорбентом. Если имеет место поглощение вещества всем объёмом фазы, то такое явление называется абсорбцией. Если оба процесса протекают одновременно, то применяют термин сорбция.

Различают физическую и химическую адсорбцию. Физическая адсорбция обусловлена молекулярными или ван -дер- ваальсовыми силами. Физическая адсорбция увеличивается с повышением концентрации (давления) адсорбата и уменьшается с повышением температуры. Тепловой эффект, сопровождающий физическую адсорбцию, соизмерим с тепловыми эффектами фазовых превращений - испарением и плавлением

Химическая адсорбция или хемосорбция обусловлена химическими (ионными, ковалентными, координационными) силами. При такой адсорбции

абсорбат образует на поверхности адсорбента химические соединения с его молекулами. Скорость химической адсорбции увеличивается с повышением температуры, что связано с наличием для химической адсорбции энергии активации. Поэтому химическую адсорбцию часто называют активированной. Химическая адсорбция также сопровождается тепловым эффектом. Его величина соизмерима с тепловыми эффектами химических реакций.

Количественно адсорбция может выражаться через различные величины:

1) Количество вещества, находящегося в объёме адсорбционного слоя, отнесённого к единице массы адсорбента. Обычно эту величину выражают

в моль/г.

2) Количество адсорбированного вещества, приходящееся на единицу площади поверхности адсорбента. Эта величина обычно выражается

в моль/м² или ммоль/см².

Адсорбция зависит температуры и концентрации растворённого вещества (давления газа).

Зависимость адсорбции от температуры при постоянной концентрации или постоянном давлении называется изобарой адсорбции: Г = f(Т) при

С = Сonst или при P = Const.

Зависимость адсорбции от концентрации растворённого вещества или давления газа называется изотермой адсорбции: Г = f(C) или Г =f(P)

при T = Const.

Одной из основных задач теории адсорбции является установление количественной связи величины адсорбции от концентрации ил давления адсорбата.

3.2Адсорбция газа (растворённого вещества)

на твёрдой поверхности.

Зависимость адсорбции газа на твёрдой поверхности от давления газа впервые была обоснована Ленгмюром. При выводе этой зависимости были использованы следующие допущения:

1) На каждом абсорбционном месте на поверхности адсорбента может только одна молекула.

2) Адсорбция является молекулярной, т.е. осуществляется только в одном слое.

3) Адсорбционная поверхность является однородной. Это означает, что все адсорбционные места на поверхности адсорбента по своим свойствам не отличаются друг от друга.

4) Между адсорбированными молекулами отсутствует взаимодействие.

С учётом этого скорость адсорбции составит:

ω₁ = k₁P(1 – Θ), (3.2)

где P – давление адсорбата;

k₁ – константа скорости процесса адсорбции;

1- Θ – доля адсорбционных мест на поверхности

адсорбента, занятых молекулами адсорбата.

Скорость процесса десорбции определится по уравнению:

ω₂ = k₂Θ, (3.4)

где k₂ – константа скорости процесса десорбции;

Θ – доля адсорбционных мест на поверхности адсорбента, занятых

молекулами адсорбата

Для условий равновесия можно записать:

ω₁ = ω₂ (3.6)

или

k₁Р(1 – Θ) = k₂Θ, (3.7)

откуда можно получить, что

Θ = 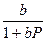, (3.8)

где b = 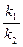- имеет смысл константы равновесия процесса адсорбции.

Если обозначить через z максимальное число адсорбционных мест на поверхности адсорбента, то адсорбция вещества на поверхности адсорбента составит:

Г = zΘ (3.9)

или

Г = 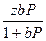(3.11)

где Г – адсорбция вещества на поверхности адсорбента.

Уравнение (3.11) представляет собой изотерму адсорбции (изотерму Ленгмюра).

При малых давления адсорбата, когда выполняется условие bР << 1.

уравнение (3.11) принимает вид:

Г = zbР (3.12)

При больших концентрациях адсорбата, когда справедливо соотношение

bC >> 1, имеет место насыщение поверхности адсорбента молекулами адсорбата, т.е. будет иметь место максимальная адсорбция:

Г = z. (3.13)

Таким образом, при мономолекулярной адсорбции максимальная адсорбция представляет собой возможное число адсорбционных мест на поверхности адсорбента.

Уравнение (3.11) можно привести к виду:

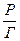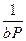= + . (3.14)

Уравнение (3.14) представляет собой прямую линию в координатах -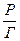

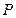
(Рисунок 3.1), что позволяет рассчитывать постоянные z и b в уравнении изотермы адсорбции на основе измерения адсорбции в зависимости от давления адсорбата.

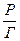
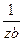
Р

Рисунок 3.1 К пояснению расчёта постоянных z и b в уравнении изотермы

адсорбции

Из графика видно, что 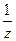= tgα, а отрезок, отсекаемый прямой на оси

ординат при Р= 0, представляет собой величину .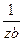

Рассуждая аналогичным образом, можно получить зависимость адсорбции растворённого вещества на поверхности твёрдого адсорбента, которая выражается уравнениями:

Г = (3.15)

Г = zbС (3.16)

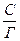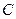= + . (3.17)

Если имеет место адсорбция из смеси газов, то для адсорбции каждого газа можно записать:

Г_i = 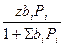(3.18)

Из уравнения (3.18) следует, что при прочих равных условиях адсорбция газа из смеси меньше, чем адсорбция из индивидуального газа.

Уравнение изотермы асорбции Ленгмюра (3.11) и (3.15) можно представить в виде графика:

Г

Р(С)

Рисунок 3.2 Графическое изображение изотермы адсорбции Ленгмюра

Изотерма Ленгмюра по своему виду напоминает параболу. Поэтому

Фрейдлих предложил эмпирическое уравнение для аналитического выражения зависимости адсорбции от давления (концентрации):

Г = 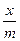= КР 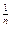(3.19)

где х – количество адсорбированного вещества;

m – масса адсорбента;

K и 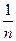- постоянные.

Для адсорбции из раствора уравнение Фрейндлиха имеет вид:

Г = 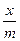= КС 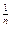, (3.20)

где С – равновесная концентрация растворенного вещества.

Логарифмирование уравнений (3.19) и (3.20) даёт:

lnГ = lnK + 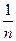P (3.21)

и

lnГ = lnK + 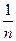С. (3.22)

Константы Фрейндлиха можно найти по изотерме, построенной в логарифмических координатах (Рисунок 6.3)

lnГ

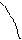
β

lnP(lnC)

Рисунок 3.3 Изотерма адсорбции в логарифмических координатах.

Тангенс угла наклона прямой к оси абсцисс представляет собой постоянную в уравнении Фрейндлиха 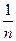, а отрезок, отсекаемый прямой на оси ординат при значении lnP (lnC) = 0, представляет постоянную lnK.

Уравнения Ленгмюра и Фрейндлиха описывают однослойную адсорбцию и справедливы для умеренных д давлений (концентраций) адсорбата. При больших значениях давлений (концентрации) эти уравнения неприменимы.

Для высоких областей давлений (концентраций) адсорбата была предложена

Эмметом и развита в работах Брунауэра и Теллера теория полимолекулярной адсорбции. Согласно этой теории адсорбция молекул адсорбата на поверхности адсорбента может осуществляться в несколько слоёв. Уравнение изотермы полимолекулярной адсорбции получило название уравнения изотермы адсорбции БЭТ. Для адсорбции газа уравнение БЭТ имеет вид:

Г = 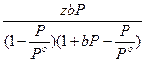(3.23)

где Р^о – давление насыщенного пара адсорбата;

- относительное давление пара.

Для адсорбции растворённого вещества уравнение БЭТ можно представить в виде:

Г = , (3.24)

где С_н – насыщенная концентрация адсорбата.

Легко видеть, что при малых давлениях или концентрациях уравнения (3.23) и (3.24) превращаются в уравнения изотермы Ленгмюра (3.11) и (3.15).

Уравнения (3.23) и (3.24) легко приводятся к линейной форме:

(3.25)

или

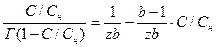(3.26)

Уравнения (6.21) и (6.22) можно представить графически:

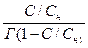
β

C/C_н

Рисунок 3.4 Графическое представление уравнения БЭТ.

где tgβ = 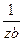, а .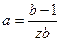

Решая систему уравнений нет, легко определить постоянные z и b в уравнении БЭТ.

Уравнение БЭТ широко используется для определения поверхности твёрдого адсорбента. Измеряя адсорбцию газа на твёрдой поверхности, по графику определяют постоянную z, которая представляет собой максимальное число адсорбционных мест на поверхности адсорбента. Зная площадь s_o, которую занимает одна молекула адсорбата, легко вычислить удельную поверхность адсорбента s_уд:

s_уд = zs_oN_A, (3.27)

где N_A – число Авогадро.

Опыты по определению удельной поверхности одного и того же адсорбента при адсорбции различных паров дают по уравнению БЭТ близкие результаты. Это подтверждает правильность толкования изотермы с помощью уравнения БЭТ. В настоящее время теория БЭТ является наиболее лучшей и полезной теорией физической адсорбции

Дата добавления: 2015-05-10