Газодинамические функции

Библиотека бесплатных электронных книг

Академік Е.К. Федоров

Газодинамические функции параметров торможения τ(λ), π(λ), ε(λ).

Зависимости между истинными параметрами состояния газа и параметрами торможения приобретают особенно удобный для расчетов вид, если их представить с помощью безразмерных скоростей М и λ. Для того чтобы получить эти зависимости, определим сначала отношения температур Т^*/Т и Т/Т^*

Отношения давлений и плотностей можно выразить с помощью уравнений изоэнтропного процесса (2.33)[1] через температуры. Тогда

(2.56)

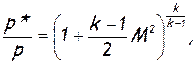(2.57)

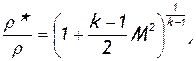(2.58)

и

(2.59)

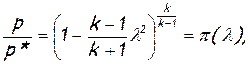(2.60)

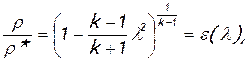(2.61)

Величины τ(λ), π(λ), и ε(λ) называются газодинамическими функциями параметров торможения. Они заранее рассчитываются для всех значений приведенной скорости λ (или числа М) и сводятся в таблицы газодинамических функций. Последние составляются для различных значений показателя изоэнтропы k, соответствующих разным газам.

Для воздуха (при k = 1,4) формулы, связывающие истинные параметры состояния с параметрами торможения, имеют следующий вид:

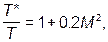(2.62)

(2.63)

(2.64)

(2.65)

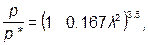(2.66)

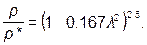(2.67)

***

Пример расчета с помощью газодинамических функций

параметров торможения

В потоке воздуха измерено:

р = 101300 н/м² (нормальное давление),

р*= 143000 н/м²,

Т* = 324 ^оК.

Определить скорость потока w.

Для воздуха показатель k=1,4; R=287,4.

1)Вычисляем .

2)По таблицам газодинамических функций для воздуха (k=1,4)

по величине π(λ)=0,7085 находим λ=0,75.

3) Определяем критическую скорость

м/сек.

4)Определяем скорость w= λa_кр=0,75∙329,6=247,2 м/сек.

Как видно из приведенного примера, весь расчет сводится к очень простым операциям. Таблицы газодинамических функций особенно эффективны при массовых расчетах.

***

Газодинамические функции потока массы (расхода) q(λ), y(λ)

В практических расчетах площадь поперечного сечения потока F и плотность тока рw удобно относить к соответствующим величинам, взятым в критическом сечении. Если, например, рассматривать сопло Лаваля, то уравнение неразрывности можно записать, приравняв расход в любом сечении расходу в критическом сечении

ρwF = ρ_кр а_кр F_кр,

в следующем виде:

(2.78)

Левая часть этого равенства — безразмерная плотность тока — называется приведенным расходом или коэффициентом расхода. Она обозначается q(λ), т.е.

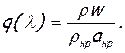(2.79)

Плотность тока рw характеризует расход газа через единицу поверхности — площади поперечного сечения. Приведенный расход представляет собой расход через единицу площади, отнесенный к расходу через единицу площади в критическом сечении. Эта величина является функцией только приведенной скорости λ и показателя изоэнтропы k. Действительно, принимая во внимание формулы (2.61) и (2.45), можно написать

или

(2.80)

По формуле (2.80) легко определяются три характерные точки:

λ=0 q(λ)=0,

λ=1 q(λ)=1,

λ= q(λ)=0.

Промежуточные значения получаются численным расчетом. График зависимости приведенного расхода от приведенной скорости представлен на рис. 23.

Наибольшая величина q(λ)=1 получается, как видим, при λ=1. Следовательно, наибольшую плотность тока газ имеет в критическом сечении. При λ<1 расход уменьшается за счет уменьшения скорости, а при λ>1 — за счет уменьшения плотности газа.

Рассматривая график на рис. 23 и формулу (2.78), легко уяснить, почему сопло Лаваля имеет такую форму. Постоянство расхода требует того, чтобы площадь канала уменьшалась в тех местах, где возрастает плотность тока, и увеличивалась там, где плотность тока падает. В том сечении, где плотность тока проходит через максимум, канал должен иметь горло. Заметим, кстати, что одной из причин невозможности достижения максимальной скорости потока является то обстоятельство, что при w=w_max, т.е. λ= , приведенный расход q(λ)=0, следовательно, площадь поперечного сечения должна была бы равняться бесконечности. Поскольку в критическом сечении плотность тока достигает максимума, то максимально возможный расход через сопло Лаваля определяется площадью горла.

С помощью функции q(λ) удобно вычислять массовый расход в любом сечении потока. Он записывается так:

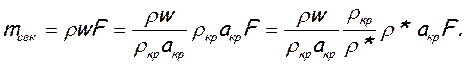
Принимая во внимание формулы (2.79), (2.45), (2.46), а также уравнение состояния совершенного газа (p=rRT), можно предыдущее выражение представить в следующем виде:

Величина

для данного газа постоянна.

Для воздуха она равна (k = 1,4; R = 287,4 дж/кг град) — m = 0,04037.

Окончательно формула расхода приобретает вид

(2.81)

Часто известной величиной бывает не р*, а статическое давление р.

Так как

то

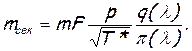
Отношение 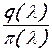для данного газа является функцией только приведенной скорости λ и обозначается y(λ). Действительно:

т.е.

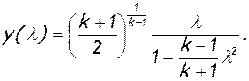(2.82)

Тогда

(2.83)

При вычислении расхода газа через сопло Лаваля или другой канал, в котором имеется критическое сечение, расчет ведется по параметрам в этом сечении. Так как в этом месте q( λ )=1, то расчетная формула имеет вид

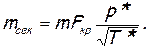(2.84)

Пример определения проходных сечений сопла Лаваля с помощью таблиц газодинамических функций.

3адано:

расход газа m_сек = 10 кг/сек;

физичеcкие константы воздуха k=1,4; R=287,4 дж/кг град,

параметры перед соплом и за ним:

p ₁* = 37,24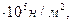

p ₂* =1,013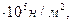

T ₁* =324°K.

Определить:

скорость истечения w₂,

площадь поперечного сечения в горле F_Г,

площадь поперечного сечения на выходе F₂.

Рассчитывается идеальный случай — энергоизолированное изоэнтропное течение, в котором соблюдаются условия постоянства давления и температуры заторможенного потока:

Т₁*= Т_Г* = Т₂* = Т*= const,

р₁*= р_Г* = р₂* = р*= const.

1.

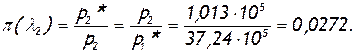
2. По таблицам газодинамических функций для k=1,4 находим при

3.

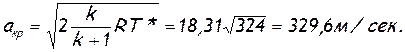
4. w₂ = a_кр λ₂ = 329,6∙1,964=647 м/сек.

5.

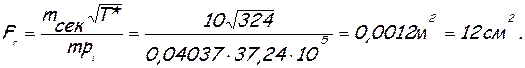
6. Так как

то

По таблицам газодинамических функций при λ₂=1,964 находим

q(λ₂)= 0,2362.

Тогда

F₂ = 0,0012 / 0,2363 = 0,00507м² = 50,7см².

Размеры всех промежуточных сечений получаются при профилировании сопла.

символ Кронекера

[1] См. файл Параметры торможения.pdf

Дата добавления: 2015-05-10