Итого 15 баллов

Балла

Балла

Баллов

Балла

Else

Begin

Begin

Пример №1.

Разработать рекурсивную процедуру для вывода на экран квадрата числа «а».

procedure KW(a: integer);

if a>0 then KW(a-1);

writeln(a*a);

end;

Условная схема, показывающая последовательность выполнения операторов для вызова процедуры KW(3):

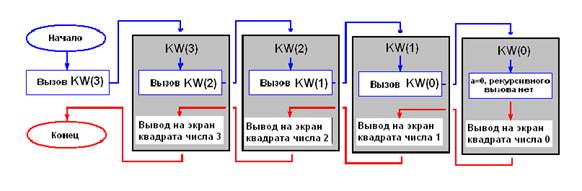
Пусть процедура KW вызывается с параметром a = 3 KW(3). В ней содержится вызов процедуры KW с параметром a = 2. Предыдущий вызов еще не завершился, поэтому создается еще одна процедура и до окончания ее работы первая свою работу не заканчивает.

Процесс вызова заканчивается, когда параметр a = 0. В этот момент одновременно выполняются 4 экземпляра процедуры: KW(3), KW(2), KW(1), KW(0). Количество одновременно выполняемых процедур называют глубиной рекурсии. В данном случае глубина рекурсии=4.

Четвертая вызванная процедура (KW(0)) напечатает число 0 и закончит свою работу. После этого управление возвращается к процедуре, которая ее вызвала (KW(1)) и печатается число 1. И так далее пока не завершатся все процедуры. Результатом исходного вызова будет печать четырех чисел:

Обратить внимание:

1. Рекурсивный вызов стоит внутри условного оператора. Это необходимое условие для того, чтобы рекурсия когда-нибудь закончилась.

if a>0 then KW(a-1);

2. Сама себя процедура вызывает с другим параметром. Вначвле KW вызывается с параметром a = 3 KW(3), каждый следующий вызов с парсметром (а-1). Если в процедуре не используются глобальные переменные, то это также необходимо, чтобы рекурсия не продолжалась до бесконечности.

Пример №2. Рекуррентные соотношения. Рекурсия и итерация. Вычисление факториала.

Простым примером величины, вычисляемой с помощью рекуррентных соотношений, является факториал

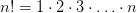
Очередной факториал можно вычислить по предыдущему как:

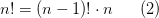
Введя обозначение , получим соотношение:

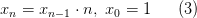
x:= 1;

for i:= 2 to n do x:=x * i;

writeln(x);

Факториал можно определить следующим образом:

Рекурсивная функция:

function Factorial(n: integer): integer;

if n > 1 then

Factorial:= n * Factorial(n-1)

Factorial:= 1;

end;

2. Выполните следующие задания:

1. Оформите программу для реализации рекурсивной процедуры из примера №1.

· Предусмотрите в программе вывод сообщения о каждом рекурсивном вызове процедуры, например

«Рекурсивный вызов процедуры для а = 3»

«Рекурсивный вызов процедуры для а = 2»

… …

и т.д.

· Предусмотрите в программе вывод сообщения о результате вычисления квадрата числа «a».

· Определите экспериментально, как изменится результат работы программы, если в процедуре поменять местамиоператорыif a>0 then KW(a-1); writeln(a*a).

1. Оформите программы для вычисления факториала числа N с использованием:

2.1. Рекурсивной функции.

2.2. Дополните таблицу операторами основной программы и продолжите заполнение таблицы трассировки программы для N=3. (При необходимости, вставьте нужные строки и столбцы в таблицу).

Functionfactorial(n: integer): longint;		N=3	N=2	N=1
begin if (N = 0) or (N = 1)		(3= 0) or (3 = 1)	(2=0) or (2=1)	(1=0) or (1=1)
then factorial:= 1				Factorial:=1
else factorial:= factorial(N - 1) * N; end; BEGIN		factorial:= factorial(3 - 1) * 3	Factorial:= Factorial(2-1)*2
read(n);
writeln(factorial(n));
END.

3. Процедура с числовыми параметрами.

Описать процедуру STEP(A,B), вычисляющую третью степень числа А и возвращающую ее в переменной В (А – входной параметр; оба параметра являются вещественными). С помощью этой процедуры найти третьи степени пяти данных чисел.

4. Функция с числовыми параметрами.

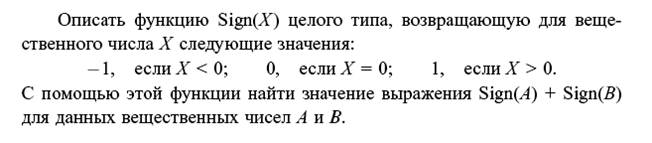
Дата добавления: 2015-05-10