Метод простой итерации

Группировка первичных данных. Составление вариационного ряда

Задание 1: Построение безынтервального вариационного ряда.

Ход работы: Получены данные о числе глазков на N клубнях картофеля. Результаты подсчета оказались следующими:

вариант	N	Число глазков
		7, 10, 5, 11, 9, 7, 8, 5, 8, 7, 7, 10, 6, 7, 5, 7, 8, 6, 5, 7, 7, 6, 5, 6, 4, 5, 5, 10, 5, 8, 7, 6, 7, 5, 7, 12, 6, 5, 6, 12.
		4, 10, 9, 9, 7, 8, 5, 8, 7, 7, 10, 6, 7, 5, 7, 8, 6, 5, 7, 7, 6, 5, 6, 4, 5, 5, 10, 5, 8, 7, 6, 7, 5, 7, 7, 6, 5, 6, 7, 4, 8
		8, 5, 8, 7, 7, 10, 6, 7, 5, 7, 8, 6, 5, 7, 7, 6, 5, 6, 4, 5, 5, 10, 5, 8, 7, 6, 7, 5, 7, 7, 6, 5, 6, 7, 4, 8, 10, 5, 6, 7, 7, 4
		10, 9, 9, 7, 8, 5, 8, 7, 7, 10, 6, 7, 5, 7, 8, 6, 5, 7, 7, 6, 5, 6, 4, 5, 5, 10, 5, 8, 7, 6, 7, 5, 7, 7, 6, 5, 6, 7, 4, 8, 10
		7, 9, 5, 11, 9, 7, 8, 5, 8, 7, 7, 10, 6, 7, 5, 7, 8, 6, 5, 7, 7, 6, 5, 6, 4, 5, 5, 10, 5, 8, 7, 6, 7, 5, 7, 7, 6, 5, 6, 6.
		10, 5, 11, 9, 7, 8, 5, 8, 7, 7, 10, 6, 7, 5, 7, 8, 6, 5, 7, 7, 6, 5, 6, 4, 5, 5, 10, 5, 8, 7, 6, 7, 5, 7, 7, 6, 5, 6, 7.
		11, 9, 7, 8, 5, 8, 7, 7, 10, 6, 7, 5, 7, 8, 6, 5, 7, 7, 6, 5, 6, 4, 5, 5, 10, 5, 8, 7, 6, 7, 5, 7, 7, 6, 5, 6, 7, 4
		9, 7, 8, 5, 8, 7, 7, 10, 6, 7, 5, 7, 8, 6, 5, 7, 7, 6, 5, 6, 4, 5, 5, 10, 5, 8, 7, 6, 7, 5, 7, 7, 6, 5, 6, 7, 6
		9, 7, 8, 5, 8, 7, 7, 10, 6, 7, 5, 7, 8, 6, 5, 7, 7, 6, 5, 6, 4, 5, 5, 10, 5, 8, 7, 6, 7, 5, 7, 7, 6, 5, 6, 7, 4, 8
		9, 5, 11, 9, 7, 8, 5, 8, 7, 7, 10, 6, 7, 5, 7, 8, 6, 5, 7, 7, 6, 5, 6, 4, 5, 5, 10, 5, 8, 7, 6, 7, 5, 7, 7, 6, 5, 6, 6.
		9, 9, 5, 11, 9, 7, 8, 5, 8, 9, 7, 10, 6, 7, 5, 7, 8, 6, 5, 7, 7, 6, 5, 6, 4, 5, 5, 10, 5, 8, 7, 6, 7, 5, 7, 7, 6, 5, 9, 9.
		9, 9, 7, 8, 5, 8, 7, 7, 10, 6, 7, 5, 7, 8, 6, 5, 7, 7, 6, 5, 6, 4, 5, 5, 10, 5, 8, 7, 6, 7, 5, 7, 7, 6, 5, 6, 7, 4, 8, 10, 5
		7, 8, 5, 8, 7, 7, 10, 6, 7, 5, 7, 8, 6, 5, 7, 7, 6, 5, 6, 4, 5, 5, 10, 5, 8, 7, 6, 7, 5, 7, 7, 6, 5, 6, 7, 4, 8, 10, 5, 6, 7, 7
		9, 7, 8, 5, 8, 7, 7, 10, 6, 7, 5, 7, 8, 6, 5, 7, 7, 6, 5, 6, 4, 5, 5, 10, 5, 8, 7, 6, 7, 5, 7, 7, 6, 5, 6, 7, 4, 8, 10, 5, 6
		8, 9, 5, 11, 9, 7, 8, 5, 8, 8, 7, 10, 6, 7, 5, 7, 8, 6, 5, 7, 7, 6, 5, 6, 4, 5, 5, 10, 5, 8, 11, 6, 2, 5, 7, 7, 6, 5, 6, 6.
		5, 11, 9, 7, 8, 5, 8, 7, 7, 10, 6, 7, 5, 7, 8, 6, 5, 7, 7, 6, 5, 6, 4, 5, 5, 10, 5, 8, 7, 6, 7, 5, 7, 7, 6, 5, 6, 7, 4

1) Найти минимальное (X _min) и максимальное (X _max) значение признака.

2) Записать все возможные значения признака и определить их частоты (f_x).

3) Составить вариационный ряд по образцу:

Значение признака x	x1	xn
Частота признака fx	fx1	fxn

4) Сделать выводы по результатам работы.

Задание 2: Построение интервального вариационного ряда.

Ход работы: Измерение длины предплечья у N особей летучей мыши вида большой трубконос Murina leucogaster Milne-Edwards без учета половой принадлежности дало следующие результаты (точность – 0,1 мм):

вариант	N	Число глазков
		39,5; 40,4; 38,6; 39,4; 39,5; 40,0; 38,6; 36,0; 39,0; 40,4; 39,5; 42,5; 41,0; 39,6; 41,8; 39,5; 40,0; 39,7; 40,0; 37,5; 42,0; 38,7; 41,5; 40,0; 42,0; 40,0; 41,5; 40,5; 37,6; 40,0; 39,5; 40,7; 40,0; 41,7; 40,0; 41,5; 41,3; 41,2; 39,0; 40,0; 40,0; 42,0; 39,3; 40,5; 39,0; 40,5; 39,5; 40,0; 39,8; 42,0; 41,2; 40,0; 39,5.
		39,4; 39,5; 40,0; 38,6; 36,0; 39,0; 40,4; 39,5; 42,5; 41,0; 39,6; 41,8; 39,5; 40,0; 39,7; 40,0; 37,5; 42,0; 38,7; 41,5; 40,0; 42,0; 40,0; 41,5; 40,5; 37,6; 40,0; 39,5; 40,7; 40,0; 41,7; 40,0; 41,5; 41,3; 41,2; 39,0; 40,0; 40,0; 42,0; 39,3; 40,5; 39,0; 40,5; 39,5; 40,0; 39,8; 42,0; 41,2; 40,0; 39,5; 40,4; 41,7.
		39,5; 40,0; 38,6; 36,0; 39,0; 40,4; 39,5; 42,5; 41,0; 39,6; 41,8; 39,5; 40,0; 39,7; 40,0; 37,5; 42,0; 38,7; 41,5; 40,0; 42,0; 40,0; 41,5; 40,5; 37,6; 40,0; 39,5; 40,7; 40,0; 41,7; 40,0; 41,5; 41,3; 41,2; 39,0; 40,0; 40,0; 42,0; 39,3; 40,5; 39,0; 40,5; 39,5; 40,0; 39,8; 42,0; 41,2; 40,0; 39,5; 40,4; 41,7.
		41,7; 39,5; 40,0; 38,6; 36,0; 39,0; 40,4; 39,5; 42,5; 41,0; 39,6; 41,8; 39,5; 40,0; 39,7; 40,0; 37,5; 42,0; 38,7; 41,5; 40,0; 42,0; 40,0; 41,5; 40,5; 37,6; 40,0; 39,5; 40,7; 40,0; 41,7; 40,0; 41,5; 41,3; 41,2; 39,0; 40,0; 40,0; 42,0; 39,3; 40,5; 39,0; 40,5; 39,5; 40,0; 39,8; 42,0; 41,2; 40,0; 39,5; 40,4; 41,7.
		36,7; 39,5; 40,0; 38,6; 36,0; 39,0; 40,4; 39,5; 42,5; 41,0; 39,6; 41,8; 39,5; 40,0; 39,7; 40,0; 37,5; 42,0; 38,7; 41,5; 40,0; 42,0; 40,0; 41,5; 40,5; 37,6; 40,0; 39,5; 40,7; 40,0; 41,7; 40,0; 41,5; 41,3; 41,2; 39,0; 40,0; 40,0; 42,0; 39,3; 40,5; 39,0; 40,5; 39,5; 40,0; 39,8; 42,0; 41,2; 40,0; 39,5; 40,4; 41,7.
		40,4; 38,6; 39,4; 39,5; 40,0; 38,6; 36,0; 39,0; 40,4; 39,5; 42,5; 41,0; 39,6; 41,8; 39,5; 40,0; 39,7; 40,0; 37,5; 42,0; 38,7; 41,5; 40,0; 42,0; 40,0; 41,5; 40,5; 37,6; 40,0; 39,5; 40,7; 40,0; 41,7; 40,0; 41,5; 41,3; 41,2; 39,0; 40,0; 40,0; 42,0; 39,3; 40,5; 39,0; 40,5; 39,5; 40,0; 39,8; 42,0; 41,2; 40,0; 39,5; 40,4.
		39,5; 40,0; 38,6; 36,0; 39,0; 40,4; 39,5; 42,5; 41,0; 39,6; 41,8; 39,5; 40,0; 39,7; 40,0; 37,5; 42,0; 38,7; 41,5; 40,0; 42,0; 40,0; 41,5; 40,5; 37,6; 40,0; 39,5; 40,7; 40,0; 41,7; 40,0; 41,5; 41,3; 41,2; 39,0; 40,0; 40,0; 42,0; 39,3; 40,5; 39,0; 40,5; 39,5; 40,0; 39,8; 42,0; 41,2; 40,0; 39,5; 40,4; 43,7; 42,5.
		40,0; 38,6; 36,0; 39,0; 40,4; 39,5; 42,5; 41,0; 39,6; 41,8; 39,5; 40,0; 39,7; 40,0; 37,5; 42,0; 38,7; 41,5; 40,0; 42,0; 40,0; 41,5; 40,5; 37,6; 40,0; 39,5; 40,7; 40,0; 41,7; 40,0; 41,5; 41,3; 41,2; 39,0; 40,0; 40,0; 42,0; 39,3; 40,5; 39,0; 40,5; 39,5; 40,0; 39,8; 42,0; 41,2; 40,0; 39,5; 40,4; 41,7; 37,6.
		40,0; 40,0; 38,6; 36,0; 39,0; 40,4; 39,5; 42,5; 41,0; 39,6; 41,8; 39,5; 40,0; 39,7; 40,0; 37,5; 42,0; 38,7; 41,5; 40,0; 42,0; 40,0; 41,5; 40,5; 37,6; 40,0; 39,5; 40,7; 40,0; 41,7; 40,0; 41,5; 41,3; 41,2; 39,0; 40,0; 40,0; 42,0; 39,3; 40,5; 39,0; 40,5; 39,5; 40,0; 39,8; 42,0; 41,2; 40,0; 39,5; 40,4; 43,7; 42,5; 39,9.
		40,3; 40,0; 38,6; 36,0; 39,0; 40,4; 39,5; 42,5; 41,0; 39,6; 41,8; 39,5; 40,0; 39,7; 40,0; 37,5; 42,0; 38,7; 41,5; 40,0; 42,0; 40,0; 41,5; 40,5; 37,6; 40,0; 39,5; 40,7; 40,0; 41,7; 40,0; 41,5; 41,3; 41,2; 39,0; 40,0; 40,0; 42,0; 39,3; 40,5; 39,0; 40,5; 39,5; 40,0; 39,8; 42,0; 41,2; 40,0; 39,5; 40,4; 43,7; 42,5.
		38,6; 36,0; 39,0; 40,4; 39,5; 42,5; 41,0; 39,6; 41,8; 39,5; 40,0; 39,7; 40,0; 37,5; 42,0; 38,7; 41,5; 40,0; 42,0; 40,0; 41,5; 40,5; 37,6; 40,0; 39,5; 40,7; 40,0; 41,7; 40,0; 41,5; 41,3; 41,2; 39,0; 40,0; 40,0; 42,0; 39,3; 40,5; 39,0; 40,5; 39,5; 40,0; 39,8; 42,0; 41,2; 40,0; 39,5; 40,4; 43,7; 42,5; 39,9
		38,6; 39,4; 39,5; 40,0; 38,6; 36,0; 39,0; 40,4; 39,5; 42,5; 41,0; 39,6; 41,8; 39,5; 40,0; 39,7; 40,0; 37,5; 42,0; 38,7; 41,5; 40,0; 42,0; 40,0; 41,5; 40,5; 37,6; 40,0; 39,5; 40,7; 40,0; 41,7; 40,0; 41,5; 41,3; 41,2; 39,0; 40,0; 40,0; 42,0; 39,3; 40,5; 39,0; 40,5; 39,5; 40,0; 39,8; 42,0; 41,2; 40,0; 39,5; 40,4; 41,7.
		40,0; 38,6; 36,0; 39,0; 40,4; 39,5; 42,5; 41,0; 39,6; 41,8; 39,5; 40,0; 39,7; 40,0; 37,5; 42,0; 38,7; 41,5; 40,0; 42,0; 40,0; 41,5; 40,5; 37,6; 40,0; 39,5; 40,7; 40,0; 41,7; 40,0; 41,5; 41,3; 41,2; 39,0; 40,0; 40,0; 42,0; 39,3; 40,5; 39,0; 40,5; 39,5; 40,0; 39,8; 42,0; 41,2; 40,0; 39,5; 40,4; 43,7; 42,5; 39,9.
		38,6; 36,0; 39,0; 40,4; 39,5; 42,5; 41,0; 39,6; 41,8; 39,5; 40,0; 39,7; 40,0; 37,5; 42,0; 38,7; 41,5; 40,0; 42,0; 40,0; 41,5; 40,5; 37,6; 40,0; 39,5; 40,7; 40,0; 41,7; 40,0; 41,5; 41,3; 41,2; 39,0; 40,0; 40,0; 42,0; 39,3; 40,5; 39,0; 40,5; 39,5; 40,0; 39,8; 42,0; 41,2; 40,0; 39,5; 40,4; 41,7; 37,6; 39,2
		39,9; 38,6; 36,0; 39,0; 40,4; 39,5; 42,5; 41,0; 39,6; 41,8; 39,5; 40,0; 39,7; 40,0; 37,5; 42,0; 38,7; 41,5; 40,0; 42,0; 40,0; 41,5; 40,5; 37,6; 40,0; 39,5; 40,7; 40,0; 41,7; 40,0; 41,5; 41,3; 41,2; 39,0; 40,0; 40,0; 42,0; 39,3; 40,5; 39,0; 40,5; 39,5; 40,0; 39,8; 42,0; 41,2; 40,0; 39,5; 40,4; 41,7; 37,6; 39,2
		39,4; 39,5; 40,0; 38,6; 36,0; 39,0; 40,4; 39,5; 42,5; 41,0; 39,6; 41,8; 39,5; 40,0; 39,7; 40,0; 37,5; 42,0; 38,7; 41,5; 40,0; 42,0; 40,0; 41,5; 40,5; 37,6; 40,0; 39,5; 40,7; 40,0; 41,7; 40,0; 41,5; 41,3; 41,2; 39,0; 40,0; 40,0; 42,0; 39,3; 40,5; 39,0; 40,5; 39,5; 40,0; 39,8; 42,0; 41,2; 40,0; 39,5; 40,4; 41,7; 40,0.

1) Найти минимальное (X _min) и максимальное (X _max) значение признака.

2) Определить величину классового интервала (l) по формуле:

l = x_max – x_min / k, где k – приблизительное число классов, на которое следует разбить вариацию признака. При числе наблюдений n от 30 до 100 число классов может равняться 7.

3) Получить классовые интервалы, приняв за середину первого интервала минимальное значение признака (X _min).

4) Уменьшить верхние границы классов на точность измерений (0,1 мм) и построить вариационный ряд по образцу:

Классовые интервалы x	x1min – x1max	xnmin - xnmax
Центральная величина классового интервала	x1	xn
Частота fx	fx1	fxn

Примечание: середину каждого классового интервала находят отношением суммы значений нижней и верхней границы интервала к 2.

5) Графически отобразить полученные данные в виде гистограммы вариационного ряда.

Нелинейное уравнение 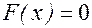всегда можно преобразовать к виду

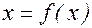, который легко сводится к следующему итерационному процессу:

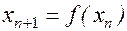, где 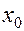задаётся. (1)

Выход из последовательных приближений можно задать условием:

.

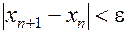(2)

Данный метод накладывает дополнительные условия на функцию 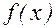. Для сходимости итерационного процесса необходимо, чтобы функция переводила отрезок 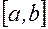внутрь себя (принцип сжатых отображений).

Пример программы на для уравнения

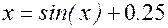(3)

10 k = 0

20 PRINT "x,E="

21 INPUT x

22 IF x = -10 THEN 300

23 INPUT e

24 PRINT " x=", x

25 PRINT " E= ", e

REM ******************************************

30 GOSUB 70

40 IF ABS(f - x) < e THEN 60

50 LET x = f

51 GOTO 30

60 PRINT "ROOT =", x, " k=", k

300 END

70 LET f = SIN(x) +.25

71 k = k + 1

72 RETURN

2. Метод Ньютона для .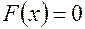

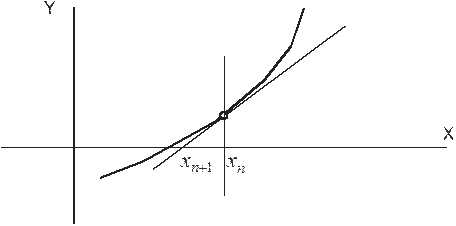
Если, следующее приближение 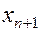, определять с помощью касательной, то нахождение корня существенно ускоряется. Уравнение касательной:

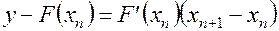, (4)

приравниваем 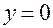- получаем

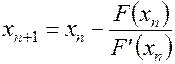. (5)

Пример программы на для уравнения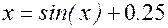

1 REM------------------------------- NEWTON01.BAS ------------------------

3 REM

4 REM Newton iter

5 REM **********************************************

6 k = 0

20 PRINT "x,E="

21 INPUT x

22 IF x = -10 THEN 300

23 INPUT e

PRINT " x=", x

PRINT " E= ", e

REM ******************************************

30 GOSUB 70

40 IF ABS(f) < e THEN 60

50 x1 = x - f

55 x2 = x

56 x = x1

57 GOTO 30

60 PRINT "ROOT =", x, " k=", k

61 END

70 f = (x - SIN(x) -.25) / (1 - COS(x))

75 k = k + 1

80 IF k > 100 THEN 61

90 RETURN

3. Модифицированный метод Ньютона для .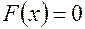

Иногда не очень удобно аналитически определять производную 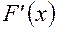, тогда можно применить численное приближение:

.

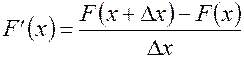В качестве 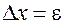из (2).

Пример программы на 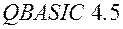для уравнения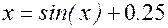

1 REM----------------------- NEWTM01.BAS ------------

3 REM

4 REM Newton modif iter

5 REM **********************************************

6 k = 0

20 PRINT "x,E="

21 INPUT x

22 IF x = -10 THEN 65

23 INPUT e

24 PRINT " x=", x

25 PRINT " E= ", e

26 REM ******************************************

30 GOSUB 70

31 LET L = f

32 LET x = x + e

40 GOSUB 70

50 L = e * L / (f - L): x = x - L - e

55 IF ABS(L) > e THEN 30

60 PRINT "ROOT =", x, " k=", k

65 END

70 f = x - SIN(x) -.25

75 k = k + 1

80 IF k > 100 THEN 300

90 RETURN

Корень данного уравнения (3)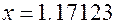

4. Определение корня уравнения делением отрезка пополам.

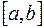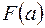Находим такой отрезок , где и 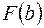были бы разного знака. Тогда делим отрезок пополам и выбирает ту половину, где знаки фукнции разные, и т.д, пока не удовлетворяется условие малости разности приближений.

10 REM Delenie popolam

15 DEF FND (X) = EXP(X) - X - 2

20 A = 0: B = 2: EPS =.000001: K = 0

30 X = (A + B) / 2

40 IF FND(A) * FND(X) > 0! THEN

A = X

41 ELSE

B = X

42 END IF

50 IF ABS(A - B) < EPS THEN 70

51 K = K + 1: IF K > 100 THEN 80

60 GOTO 30

70 PRINT " Root X= ", X, " Iter = ", K

80 END

Дата добавления: 2015-05-10