Касательная плоскость и нормаль к поверхности

КАРТА 12.

ТЕМА: ПЕРИНАТАЛЬНАЯ ПАТОЛОГИЯ

1. Характеристика болезни гиалиновых мембран:

а) В каком гестационном возрасте чаще развивается

б) Основные патогенетические факторы 1-4

в) Макроскопическая картина 1-3

г) Микроскопическая картина 1-4

д) Стадии развития мембран 1-3

е) Осложнения 1-3

2. Соедините попарно заболевание и его клиническое проявление:

1. Поднадкостничное кровоизлияние в своде черепа А. Паралич Эрба-Дюшена

2. Родовая травма нервов плечевого сплетения Б. Кровоизлияние в полость черепа

3. Разрыв спинного мозга В. Паралич Дежерин-Клюмпке

4. Разрыв вены Галена Г. Кефалогематома

5. Массивная аспирация Д. Синдром дыхательной

мекония недостаточности

3.Причины интранатальной гипоксии плода (выбрать правильные ответы):

а) истинные узлы пуповины, б) пороки развития плаценты, в) абсолютно короткая

пуповина, г) инфекционные заболевания плода, д) преждевременная отслойка плаценты.

4. У доношенного новорожденного, рожденного при стремительных родах, обнаружено

ассиметричное увеличение мягких тканей головы в правой теменной области. При пунктировании

данного образования было извлечено 100 мл жидкой крови.

а) Диагноз?

б) К какой группе заболеваний относится выявленная патология?

в) Патогенез 1-2

г) Осложнения 1-3

Рассмотрим одно из геометрических приложений частных производных функции двух переменных. Пусть функция 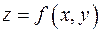дифференцируема в точке 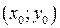некоторой области 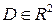. Рассечем поверхность 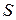, изображающую функцию , плоскостями 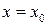и .

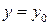Плоскость 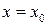пересекает поверхность 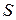по некоторой линии 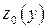, уравнение которой получается подстановкой в выражение исходной функции 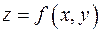вместо 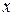числа 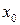. Точка 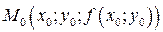принадлежит кривой 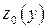. В силу дифференцируемости функции в точке 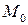функция 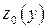также является дифференцируемой в точке 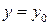. Следовательно, в этой точке в плоскость 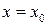к кривой касательная .

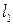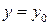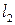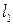Проводя аналогичные рассуждения, для сечения построим касательную к кривой . Прямые и 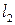определяют плоскость 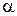, которая называется касательной плоскостью к поверхности 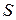в точке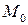

Составим её уравнение. Так как плоскость 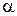проходит через точку 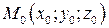, то её уравнение может быть записано в виде

,

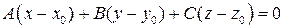которое можно переписать так:

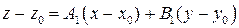(1)

(разделив уравнение на 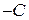и обозначив ).

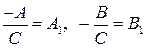Найдем 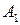и .

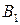Уравнения касательных 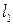и 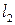имеют вид

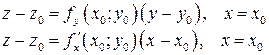
соответственно.

Касательная 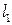лежит в плоскости 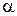, следовательно, координаты всех точек 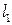удовлетворяют уравнению (1). Этот факт можно записать в виде системы

.

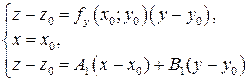Разрешая эту систему относительно 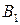, получим, что .

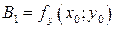Проводя аналогичные рассуждения для касательной 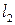, легко установить, что .

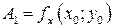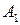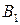Подставив значения и в уравнение (1), получаем искомое уравнение касательной плоскости:

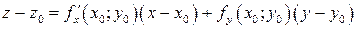(2)

Прямая, проходящая через точку 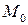и перпендикулярная касательной плоскости, построенной в этой точке поверхности, называется её нормалью.

Используя условие перпендикулярности прямой и плоскости легко получить каноническое уравнение нормали:

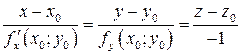(3)

Если поверхность 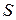задана уравнением 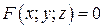, то уравнения (2) и (3), с учетом того, что частные производные могут быть найдены как производные неявной функции:

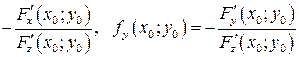
Замечание. Формулы касательной плоскости и нормали к поверхности получены для обыкновенных, т.е. не особых, точек поверхности. Точка 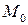поверхности называется особой, если в этой точке все частные производные равны нулю или хотя бы одна из них не существует. Такие точки мы не рассматриваем.

Пример 1. Написать уравнение касательной плоскости и нормали к параболоиду вращения 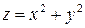в точке .

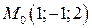Решение: Здесь 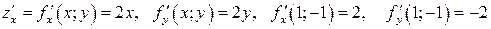. Пользуясь формулами (2) и (3) получаем уравнение касательной плоскост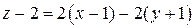и: или 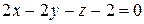и уравнение нормали: .

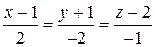Дата добавления: 2015-05-10