Построить полигон частот

Решение.

Строим точки основываясь на данных из таблицы. Полученные точки соединяем отрезками прямой. Обратите внимание на точки (0; 0) и (13; 0), расположенные на оси абсцисс и имеющие своими абсциссами числа, на 1 меньшее и большее, чем соответственно абсциссы самой левой и самой правой точек. Полигон частот изображен на рисунке.

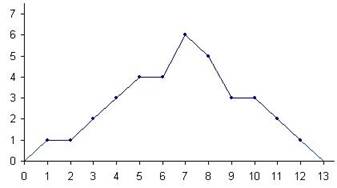
Если полигон строят по данным интервального ряда, то в качестве абсцисс точек берут середины соответствующих интервалов. Крайние левую и правую точки соединяют с точками оси абсцисс - серединами ближайших интервалов, частоты которых равны нулю. Конечно, в этом случае полигон лишь приближенно отображает зависимость частот от значений аргумента.

Кумулята служит для графического изображения кумулятивного вариационного ряда. Для ее построения на оси абсцисс откладывают значения аргумента, а на оси ординат - накопленные частоты или накопленные относительные частоты. Масштаб на каждой оси выбирают произвольно. Далее строят точки, абсциссы которых равны вариантам (в случае дискретных рядов) или верхним границам интервалов (в случае интервальных рядов), а ординаты - соответствующим частотам (накопленным частотам). Эти точки соединяют отрезками прямой. Полученная ломаная и является кумулятой.

Пример построения кумуляты

По данным таблицы составить кумулятивный вариационный ряд, для которого построить кумуляту.

Количество баллов x

Число учащихся n

Решение.

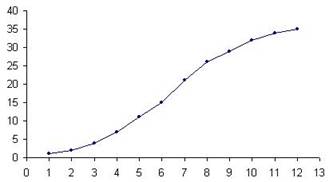
Cоставим кумулятивный вариационный ряд (см. таблицу ниже), для которого построим кумуляту.

Количество баллов

Частота

Накопленная частота n

Гистограмму используют для изображения интервальных рядов. Для построения гистограммы по данным вариационного ряда с равными интервалами, как и для построения полигона, на оси абсцисс откладывают значения аргумента, а на оси ординат - значения частот или относительных частот. Далее строят прямоугольники, основаниями которых служат отрезки оси абсцисс, длины которых равны длинам интервалов, а высотами - отрезки, длины которых пропорциональны частотам или относительным частотам соответствующих интервалов.

В результате получают ступенчатую фигуру в виде сдвинутых друг к другу прямоугольников, площади которых пропорциональны частотам (или относительным частотам).

Если интервалы неравные, то на оси ординат следует откладывать в произвольно выбранном масштабе значения плотности распределения (абсолютной или относительной). Таким образом, высоты прямоугольников, которые мы строим, должны равняться плотностям соответствующих интервалов.

При графическом изображении вариационного ряда с помощью гистограммы плотность изображается так, как если бы она оставалась постоянной внутри каждого интервала. На самом деле, как правило, это не так. Если построить распределение по частям интервалов, то можно убедиться в том, что плотность распределения на различных участках интервала не остается постоянной. Плотность, полученная ранее, представляла лишь некоторую среднюю плотность. Итак, гистограмма изображает не фактическое изменение плотности распределения, а лишь средние плотности распределения на каждом интервале.

Если построена гистограмма интервального распределения, то полигон того же распределения можно получить, если соединить прямолинейными отрезками середины верхних оснований прямоугольников.

Пример построения гистограммы

По результатам тестирования по математике учащихся 7-го класса получены данные о доступности заданий теста (отношение числа учащихся, правильно выполнивших задания, к числу тестировавшихся учащихся), предствленные ниже, в таблице.
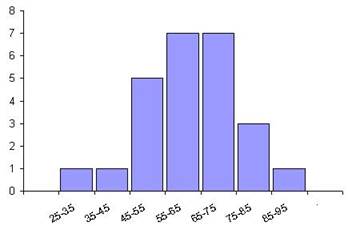
Тест содержал 25 заданий. Построить гистограмму.

Доступность задания x, %	25-35	35-45	45-55	55-65	65-75	75-85	85-95
Количество задач n

Решение.

Откладываем на оси абсцисс 7 отрезков длиной 10. На них, как на основаниях, строим прямоугольники, высоты которых соответственно равны 1, 1, 5, 7, 7, 3, 1. Полученная ступенчатая фигура и является искомой гистограммой.

Пример построения гистограммы

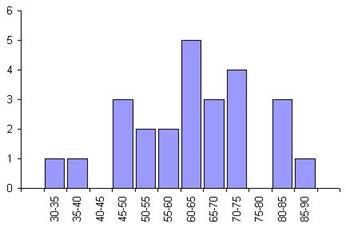
Данные, приведенные в предыдущем примере представим более подробно (см. таблицу ниже.). Построить гистограмму.

Доступность задания x, %	30-35	35-40	40-45	45-50	50-55	55-60
Количество задач n
Доступность задания x, %	60-65	65-70	70-75	75-80	80-85	85-90
Количество задач n

Решение.

Далее на рисунке построена гистограмма по этим данным. Получено изображение более подробной информации о распределении данных.

Дата добавления: 2015-05-10