Краткая теория

Владивосток

Определение фокусных расстояний собирающей и рассеивающей линз по методу Бесселя

ЛАБОРАТОРНАЯ РАБОТА № 1.1

END.

BEGIN

Begin

Begin

Write(' Введите длину массива');

Readln(K);

Writeln(' Введите элементы массива целых чисел, через пробел');

For i:=1 to K do Read(M[i]);

readln;

End; { конец процедуры ввода}

{ Процедура поиска максимального элемента в массиве}

Procedure Poisk_max(K:integer; M:Tmas; Var Max:integer);

Var i:integer;

Max:=M[1]; { За максимум принимаем первый элемент}

For i:=2 to K do

If M[i]>Max then Max:=M[i]; {Запоминаем новый максимум}

End;

{ Начало основной программы}

Clrscr;

Writeln(' Ввод первого массива'); Vvod(K1, M1);

Writeln(' Ввод второго массива'); Vvod(K2, M2);

Poisk_max(K1, M1, Max1); Poisk_max(K2, M2, Max2);

If Max1>Max2 then writeln(' Max1 больше и оно = ',Max1)

else writeln(' Max2 больше и оно = ',Max2);

Readkey; { Останов для просмотра результатов}

Типовое задание

Для задания из лабораторной работы №11 разработать программу с использованием процедур: оформить в виде процедур каждый из пунктов задания.

ЛИТЕРАТУРА

1. Игошина Л.В. Методическое пособиепо курсу "Алгоритмические языки и программирование". - Пенза: ПГТУ, 1999г.
2. Могилев Л.В. и др. Практикум по информатике. - М.: «Академия», 2005г.
3. Иллюстрированный самоучитель по Turbo Pascal. – http://pascal.sources.ru/

Цель работы: изучение свойств собирающих и рассеивающих линз и их систем, ознакомление с методом Бесселя, определение фокусного расстояния линзы.

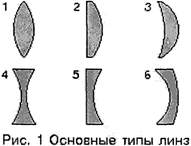
Линзой называется прозрачное для света тело, ограниченное двумя сферическими поверхностями. Основные виды линз представлены на рис.1.

Собирающие (в воздухе):

1 – двояковыпуклая линза,

2 – плоско-выпуклая линза,

3 – вогнуто-выпуклая линза.

Рассеивающие (в воздухе):

4 – двояковогнутая линза,

5 – плоско-вогнутая линза,

6 – выпукло-вогнутая линза.

Тонкой называется линза, толщина которой намного меньше любого из ее радиусов кривизны.

Оптическая система называется центрированной, если центры кривизны всех ее преломляющих поверхностей лежат на одной прямой, называемой главной оптической осью системы. Точка пересечения плоскости линзы с оптической осью называется оптическим центром тонкой линзы. Любая прямая, проходящая через оптический центр линзы и не совпадающая с главной оптической осью, называется побочной оптической осью.

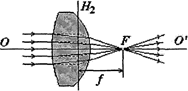
Если на собирающую линзу падают лучи, параллельные главной оптической оси, то они, после преломления в линзе, пересекаются в одной точке, лежащей на главной оптической оси и называемой главным фокусом линзы F (рис. 2). У линзы имеется два главных фокуса по обе стороны от нее. Расстояние f от оптического центра до фокуса называется фокусным расстоянием. Если радиусы кривизны поверхностей линзы одинаковы и с обеих сторон от линзы среда одна и та же, то фокусные расстояния линзы одинаковы.

Рис. 2. Ход лучей в собирающей линзе.

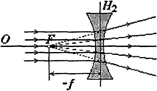
Если на рассеивающую линзу падают лучи, параллельные главной оптической оси, то в одной точке, также называемой главным фокусом, пересекаются не сами преломленные лучи, а их продолжения (рис.3). Фокус в этом случае называется мнимым, а фокусное расстояние считается отрицательным. У рассеивающей линзы также два главных фокуса по обе стороны от нее.

Рис. 3. Ход лучей в рассеивающей линзе.

Плоскость, проходящая через главный фокус линзы перпендикулярно главной оптической оси, называется фокальной плоскостью, а точка пересечения какой-либо побочной оси с фокальной плоскостью называется побочным фокусом. Если на линзу падает пучок лучей, параллельных какой-то побочной оси, то после преломления либо сами лучи, либо их продолжения (в зависимости от вида линзы) пересекаются в соответствующем побочном фокусе. Лучи, идущие через оптический центр тонкой линзы, своего направления практически не меняют.

Построение изображения в линзах. Для построения изображения светящейся точки из этой точки надо взять не менее двух лучей, падающих на линзу, и построить ход этих лучей. Как правило, выбираются лучи, параллельные главной оптической оси, проходящие через главный фокус линзы, или идущие через оптический центр линзы. Пересечение этих лучей, либо их продолжений, дает действительное или мнимое изображение точки. Для получения изображения отрезка строят изображения его крайних точек. Если светящийся предмет – небольшой отрезок, перпендикулярный главной оптической оси, то его изображение тоже будет представляться отрезком, перпендикулярным главной оптической оси. Проще всего построить изображение отрезка, одна из двух крайних точек которого лежит на главной оптической оси: в этом случае строится изображение другой его крайней точки и опускается перпендикуляр на главную оптическую ось (рис. 4). Для построения изображений также могут быть использованы побочные оптические оси и побочные фокусы. В зависимости от вида линзы и положения предмета относительно линзы изображение может быть увеличенным или уменьшенным.

При построении изображений используют условные изображения тонкой линзы:

↕ - двояковыпуклая линза, ‍‍‍‍↕ - двояковогнутая линза

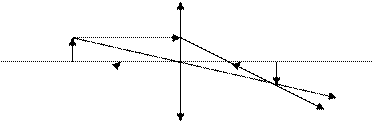
Рис. 4а. Построение действительного изображения в тонкой собирающей линзе (предмет находится за фокусом).

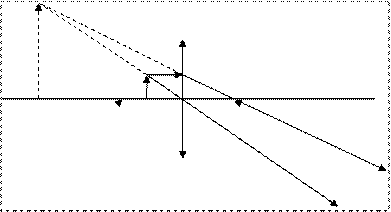
Рис. 4б. Построение мнимого изображения в тонкой собирающей линзе (предмет находится между фокусом и линзой).

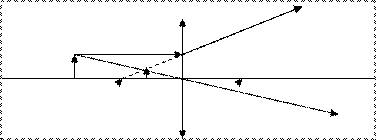
Рис. 4в. Построение мнимого изображения в тонкой рассеивающей линзе (предмет находится за фокусом).

Формула линзы. Если обозначить расстояние от предмета до линзы – s, а расстояние от линзы до изображения - s′, то формулу тонкой линзы можно записать в виде:

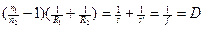
где R₁ и R₂ – радиусы кривизны сферических поверхностей линзы, n₁ – показатель преломления вещества, из которого сделана линза, n₂ – показатель преломления среды, в которой находится линза.

Величина D, обратная фокусному расстоянию линзы, называется оптической силой линзы и измеряется в диоптриях. У собирающей линзы оптическая сила положительна, у рассеивающей – отрицательна.

Другой важный параметр линзы – линейное увеличение Г. Оно показывает, чему равно отношение линейного размера изображения h′ к соответствующему размеру предмета h. Можно показать, что Г=h′/h=s′/s.

Дата добавления: 2015-05-10