
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные теоретические положения. Измерения, при котором искомое значение величин находят на основании известной зависимости между этой величиной и величинами
Измерения, при котором искомое значение величин находят на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям, называются косвенным.
Допустим, определяется величина путем непосредственного измерения величин x1,x2,…,xm, с которыми связана зависимость
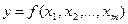
| (2.1) |
Если результаты прямых измерений x1,x2,…,xm содержат случайные погрешности, они являются случайными величинами и поэтому величину, измеренную косвенно путем вычислений по результатам прямых измерений, нужно рассматривать, как функцию случайных величин. Среднее значение результата косвенных измерений находят подстановкой в функциональную зависимость (2.1) средних значений результатов прямых измерений:
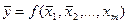
| (2.2) |
Среднеквадратичное отклонение случайной погрешности косвенного измерения:
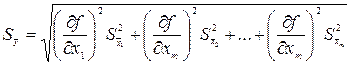
| (2.3) |
Распределение результата косвенных измерений будет нормальным, если нормальны распределения результатов прямых измерений, а их среднестатистические получены обработкой достаточно большого числа результатов.
Если же объемы рядов прямых измерений недостаточно велики, можно воспользоваться распределением Стьюдента с некоторым "Эффективным" числом степеней свободы, которые при независимости погрешности подсчитываются по формуле:
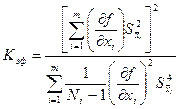
| (2.4) |
Кэф – характеризует количество измерений для y.
По значению Кэф и вероятности попадания в доверительный интервал Р находим коэффициент Стьюдента tp. Тогда доверительный интервал определяется следующим образом:
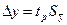
| (2.5) |
и результат косвенного измерения можно записать в виде:
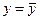 : Δ от – Δу до + Δу; Р=0,95 : Δ от – Δу до + Δу; Р=0,95
| (2.6) |
Математическое ожидание результата косвенных измерений не равно истинному значению измеряемой величины, т.е. оценка (2.2) является смещенной, если хотя бы одна вторая частная производная уравнения (2.1) отличается от 0 и погрешность результата косвенного измерения наряду со случайной, содержит систематическую составляющую.
Если погрешность измерения аргумента некоррелированы, эта систематическая погрешность определяется как:
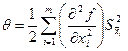
| (2.7) |
Для того чтобы исключить систематическую погрешность, нужно к рассчитанному по формуле (2.2) результату прибавить поправку q, равную систематической погрешности по величине и обратную ей по знаку. Результаты п измерений величины x обрабатываются следующим образом:
1. Определяют среднеарифметическое ряда наблюдений
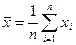
| (2.8) |
2. Вычисляют случайные отклонения результатов наблюдений
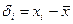
| (2.9) |
3. Вычисляют оценку среднеквадратичного отклонения ряда наблюдений
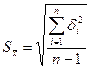
| (2.10) |
4. Вычисляют оценку среднеквадратичного отклонения результатов прямых измерений
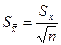
| (2.11) |
|
|
Дата добавления: 2015-05-10; Просмотров: 589; Нарушение авторских прав?; Мы поможем в написании вашей работы!