Последовательность обработки результатов при прямых измерениях

ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

Омск 2008

Обработка результатов измерений

Методические указания

Все проводимые измерения можно разделить на прямые и косвенные. а) При прямых измерениях искомая величина получается непосредственно при помощи измерительного прибора. Так называемая приборная погрешность 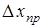определяется при этом по классу точности прибора, а если он не указан, то приборная погрешность принимается равной половине цены наименьшего деления шкалы прибора.

б) При косвенных измерениях искомая величина y не измеряется, а вычисляется по формуле через другие, непосредственно измеряемые величины x₁, x₂,…x_n, то есть, измеряемая величина является некоторой функцией одного или нескольких аргументов y = y(x_1, x_2,…x_n).

Косвенные измерения являются воспроизводимыми, если каждый аргумент при повторении измерений должен принимать одно и то же значение.

Косвенные измерения являются невоспроизводимыми, если при повторении измерений аргументы принимают заведомо разные значения.

1.1. Определить приборную погрешность .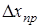

1.2. Провести измерения n раз некоторой величины 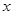, определив значения .

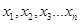1.3. Вычислить среднее арифметическое значение результатов измерений

.

1.4. Определить величины отклонений результатов измерений от среднего значения

.

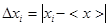1.5. Рассчитать среднеквадратичную погрешность

.

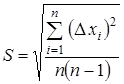1.6. Задать величину надежности измерений a и по таблице найти значение коэффициента Стьюдента .

1.7. Найти случайную погрешность измерений

.

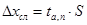1.8. Вычислить абсолютную погрешность измерений

.

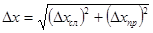1.9. Вычислить значение относительной погрешности измерений

.

1.10. Записать результат обработки данных в виде:

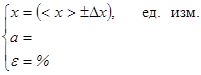
При записи окончательного результата погрешности измерений округляются до двух первых значащих цифр. Числовое значение определяемой величины должно оканчиваться цифрой того же разряда, что и значение абсолютной погрешности.

Таблица значений коэффициента Стьюдента

a/n
0,7	2,0	1,3	1,3	1,2	1,2	1,1	1,1	1,1	1,1	1,0
0,8	3,08	1,89	1,64	1,53	1,48	1,44	1,42	1,4	1,38	2,28
0,9	6,31	2,92	2,35	2,13	2,02	1,94	1,9	1,86	1,83	1,64
0,95	12,7	4,3	3,18	2,78	2,57	2,45	2,36	2,31	2,26	1,96

Дата добавления: 2015-05-10