Лагранжев формализм. Функция Лагранжа, уравнения Лагранжа, обобщенные импульс, сила, энергия. Принцип наименьшего действия

Для задания положения материальной точки в любой момент времени используется радиус вектор 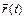. Определение зависимости 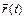для каждой материальной точки системы составляет основную задачу механики. В классической механике уравнениями движения, определяющими 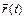, являются уравнения Ньютона

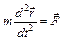. (1)

Таким образом, основная задача механики сводится к двукратному интегрированию уравнения (1). Но непосредственное интегрирование (1) не всегда является удобным способом решения. Это связано с тем, что если система состоит из N тел, то (1) будет представлять собой систему из 3N дифференциальных уравнений. Если, кроме этого, система обладает определенной симметрией, то лучше использовать вместо декартовой системы координат другую, соответствующую симметрии данной системы. Поэтому в ряде задач механики используется лагранжев формализм, при котором механической системе сопоставляется функция обобщенных координат, обобщенных скоростей и времени: 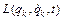, которую называют функцией Лагранжа. Обобщенными координатами q_k называют любые величины, с помощью которых может быть задано положение системы в пространстве. Обобщенными скоростями называют производные обобщенных координат по времени. Записав для системы функцию Лагранжа, можно решить основную задачи механики с помощью уравнений Лагранжа, которые заменяют уравнения Ньютона. Использование уравнений Лагранжа удобно тем, что количество этих уравнений равно числу степеней свободы системы. В случае, когда на систему наложены связи, число этих уравнений будет меньше 3N. Под связями понимают любые ограничения, наложенные на систему. На практике очень важен и часто встречается случай, когда связь может быть описана с помощью уравнения, связывающего координаты точек системы: . Такая связь называется голономной, примером голономной связи может служить жесткий невесомый стержень, связывающий две частицы.

Покажем, как от уравнений Ньютона можно перейти к лагранжеву формализму. Рассмотрим систему, состоящую из N взаимодействующих частиц с массами m ⁽¹⁾, m ⁽²⁾,…:

Введем следующие обозначения: m ₁ = m ₂ = m ₃ = m ⁽¹⁾– масса 1-ой частицы, m ₄ = m ₅ = m ₆ = m ⁽²⁾ масса 2-ой частицы,..., х ₁– координата х 1-ой частицы, х ₂– координата у 1-ой частицы, х ₃– координата z 1-ой частицы, x ₄, x ₅, x ₆ – координаты x, y, z 2-ой частицы, …, F ₁, F ₂, F ₃– проекции на оси x,y,z силы, действующей на 1-ю частицу, F ₄, F ₅, F ₆ – проекции на оси x,y,z силы, действующей на 2-ю частицу и т.д.

Если на частицы действуют потенциальные силы, то они могут быть выражены следующим образом:

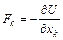, (2)

где – функция координат и времени, называемая потенциалом. Если в функцию U время явно не входит, то она называется потенциальной энергией системы.

Пусть часть сил, действующих на систему частиц потенциальна, а часть – не потенциальна, тогда уравнения движения частиц системы:

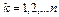(3)

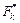– компоненты непотенциальных сил. Число n уравнений, входящих в (3), равно утроенному числу частиц системы ().

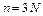Определим для данной системы функцию Лагранжа как разность кинетической и потенциальной энергии:

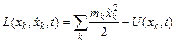. (4)

Продифференцировав по времени частную производную от L по , получим левую часть уравнения (3):

.

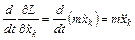Продифференцировав L по х _k, получим k-ю компоненту потенциальной силы:

.

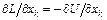Таким образом, мы приходим к уравнениям:

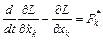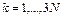, (5)

которые называются уравнения Лагранжа. Для систем, в которых действуют только потенциальные силы, уравнения Лагранжа имеют вид:

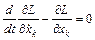. (6)

Мы получили уравнения Лагранжа (6) в декартовых координатах для системы частиц без связей. Если на систему частиц наложены связи, ограничивающие движение, то удобно ввести обобщенные координаты q_k и обобщенные скорости . При этом число обобщенных координат будет равно числу степеней свободы s <3 N. Функция Лагранжа запишется в виде 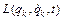. В обобщенных координатах уравнения Лагранжа запишутся аналогично (6):

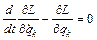(7)

Функция Лагранжа 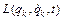может быть использована для характеристики не только систем с конечным числом степеней свободы, но и систем с бесконечным числом степеней свободы – сплошных сред, электромагнитных и других физических полей.

Из выражения для функции Лагранжа (4) следует, что производная – проекция импульса соответствующей частицы на одну из координатных осей, а 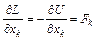– проекция потенциальной силы, действующая на частицу. Аналогично при использовании обобщенных координат величину

(8)

называют обобщенным импульсом, а величину

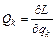(9)

- обобщенной силой.

Через функцию Лагранжа выражается также полная энергия системы.

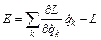(10)

(10) является самым общим выражением энергии системы и остается пригодным даже в том случае, когда полная энергия не может быть представлена в виде суммы кинетической и потенциальной энергией.

В основу механики вместо законов Ньютона можно положить принцип наименьшего действия или принцип Гамильтона. Действием S за промежуток времени [t₁, t₂] называется интеграл

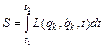(12)

Положение системы характеризуется координатами q_k (t). Согласно принципу наименьшего действия система на временном интервале [t₁, t₂] всегда движется так, что ее действие S принимает наименьшее возможное значение. Размерность действия равна Дж×с. Такую же размерность имеет постоянная Планка, которую называют также квантом действия. Принцип Гамильтона представляет собой наиболее общую формулировку закона движения механических систем. Он может быть применен не только к механическим системам, но и к упругим средам, электромагнитным полям и т.п.

Дата добавления: 2015-05-07