Электромагнитные волны в вакууме, их свойства и основные характеристики. Поляризация электромагнитных волн

Положим в дифференциальных уравнениях Максвелла плотность зарядов r и плотность токов 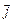равными нулю. Тогда уравнения будут описывать электромагнитное поле в вакууме:

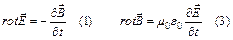
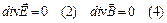
Из уравнений (2) и (4) следует, что электрическое и магнитное поля соленоидальны, т.е. линии векторов замкнуты. Источников линий электрического поля нет, и они охватывают силовые линии магнитного поля. Магнитное поле соленоидально и силовые линии магнитного поля охватывают силовые линии электрического поля. Обе компоненты электромагнитного поля взаимосвязаны. Изменение одной влечет за собой изменение другой. Взаимосвязь и конечная скорость распространения поля в пространстве приводят к образованию электромагнитной волны.

Покажем, что из уравнений Максвелла следует вывод о распространении электромагнитной волны.

Продифференцируем по времени обе части уравнения (3):

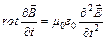(5)

Подставим в (5) (1) и учтем, что 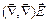= , тогда Величина , где с – скорость распространения электромагнитной волны.

(6)

Выполняя аналогичные преобразования с двумя другими уравнениями Максвелла, получим волновое уравнение для вектора :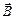

(7)

Решение волновых уравнений (6) и (7) записывается в виде плоских волн , единичный вектор указывает направление распространения волны, f ₁ – волна, распространяющаяся в направлении вектора , f ₂ – волна, распространяющаяся в противоположном направлении. Во многих случаях на практике имеет место только волна, распространяющаяся от источника, поэтому решение представляют в виде функции, зависящей только от аргумента :

(8)

Из уравнений Максвелла можно также получить следующие свойства электромагнитных волн.

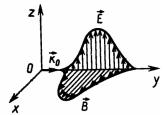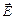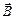1. Электромагнитные волны в вакууме поперечные, т.е. и перпендикулярны направлению распространения .

2. В электромагнитной волне . Модули векторов связаны соотношением

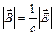. (9)

Характеристикой электромагнитной волны является плотность потока энергии (вектор Пойтинга)

. (10)

. Модуль вектора Пойтинга равен энергии, переносимой за единицу времени через единицу площади поверхности, перпендикулярной к направлению распространения электромагнитной волны.

В заданном объеме V электромагнитная волна обладает энергией:

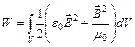(11)

Формулы (8) с условием (9) описывают плоские волны напряженности и индукции, распространяющиеся в пространстве со скоростью с.

Важное значение имеет частный случай плоских волн – плоские монохроматические волны:

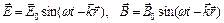, где , 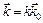. (12)

В общем случае электромагнитная волна может быть представлена суперпозицией плоских монохроматических волн всевозможных частот, амплитуд и направлений.

Частными решениями уравнений (6) и (7) являются функции вида

и

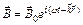
Электромагнитная волна с векторам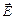и и 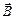, направление которых определено в любой момент времени, называется поляризованной. Если направление векторов 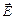и 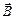изменяется случайным образом, то электромагнитная волна называется неполяризованной.

Плоскость, проходящая через направление распространения волны 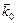и вектор 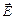, называется плоскостью поляризации.

Если положение плоскости поляризации остается неизменным, то волна будет плоско поляризованной. Для плоскополяризованной волны может быть несколько состояний поляризации: эллиптическая, круговая, линейная. Так, уравнения (12) описывают линейно поляризованную волну, т.к. конец вектора 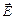движется по прямой линии. Если конец вектора 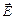описывает в плоскости эллипс, то это волна с эллипической поляризацией, в волне с круговой поляризацией конец вектора 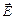описывает круг.

Дата добавления: 2015-05-07