Вычисление стандартной неопределенности (uB) по типу В

Вычисление стандартной неопределенности (uA) по типу А

Исходными данными для вычисления являются результаты многократных измерений: x_i1,…,x_ini (i=1,…,m), где n_i – число измерений i -й входной величины. Стандартную неопределенность единичного измерения i -й входной величины вычисляют по формуле:

u_A,t = (10.1)

где 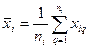– среднее арифметическое результатов измерений i -й входной величины.

Стандартную неопределенность измерений i -й входной величины, при которых результат определяют как среднее арифметическое, вычисляют по формуле:

u_A(x_I) = 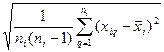(10.2)

Исходными данными для вычисления является следующая информация:

· данные предшествовавших измерений величин, входящих в уравнение измерения; сведения о виде распределения вероятностей;

· данные, основанные на опыте исследователя или общих знаниях о поведении и свойствах соответствующих приборов и материалов;

· неопределенности констант и справочных данных;

· данные поверки, калибровки, сведения изготовителя о приборе и др.

Неопределенности этих данных обычно представляют в виде границ отклонения значений величины от ее точечной оценки. При неполном знании о неопределенности некоторой i-й входной величины обычно постулируют равновероятное распределение возможных значений этой величины в указанных (нижней и верхней) границах [b_i-, b_i+]. При этом стандартную неопределенность, вычисляемую по типу В, определяют по формуле:

u_B(x_i) = 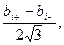(10.3)

а для симметричных границ (±b_i) –

u_B(x_i) = 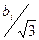. (10.4)

В случае других законов распределения формулы для вычисления неопределенности по типу В будут иными.

Вычисление суммарной стандартной неопределенности (u_c)

Оценку дисперсии суммарной стандартной неопределенности при некоррелированных результатах измерений x₁,…, x_m получают из зависимости:

u_c²(y) = 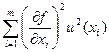(10.5)

В случае коррелированных результатов измерений x₁,…, x_m оценку вычисляют по формуле:

u_c²(y) = 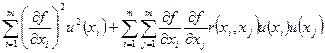(10.6)

где r(x_i, x_j) – коэффициент корреляции, u(x) – стандартная неопределенность входной величины, вычисленная по типу А или по типу В.

Для вычисления коэффициента корреляции используют согласованные пары результатов измерений (x_il, x_jl) (l=1,…n_ij, где n_ij – число согласованных результатов измерений):

r(x_i, x_j) = 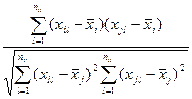(10.7)

Выбор коэффициента охвата k при вычислении расширенной неопределенности

В общем случае коэффициент охвата выбирают в соответствии с формулой:

k = t_p(v_eff) (10.8)

где t_p(v_eff) – квантиль распределения Стьюдента с эффективным числом степенен свободы v_eff и доверительной вероятностью (уровнем доверия) р. Значения коэффициента t_p(v_eff) приведены в приложении Г Руководства.

Число степеней свободы определяют по формуле:

v_eff = , (10.9)

где v_i - число степеней свободы при определении оценки i -й входной величины:

v_i = n_i – 1 для вычисления неопределенностей по типу А;

v_i =∞ для вычисления неопределенностей по типу В.

Во многих практических случаях при вычислении неопределенностей измерений делают предположение о нормальном законе распределения возможных значений измеряемой величины и полагают:

k = 2 при р ≈ 0,95 и k = 3 при р ≈ 0,99.

При допущении распределения данных по закону равной вероятности полагают:

k = 1,65 при р ≈ 0.95 и k = 1,71 при р ≈ 0,99.

При представлении результатов измерений Руководство рекомендует приводить достаточное количество информации для возможности проанализировать или повторить весь процесс получения результата измерений и вычисления неопределенностей измерений, а именно:

· алгоритм получения результата измерений.

· алгоритм расчета всех поправок и их неопределенностей;

· неопределенности всех используемых данных и способы их получения:

· алгоритмы вычисления суммарной и расширенной неопределенностей (включая значение коэффициента k).

ВНИИМ им. Д.И.Менделеева в 1999 году разработал нормативный документ ГСИ. Рекомендация МИ 2552 – 99 «Применение "Руководства по выражению неопределенности измерений"», цель которого ясна из названия. Позже этот документ был заменен межгосударственными рекомендациями РМГ 43 – 2001 с тем же названием. В РМГ 43 изложены основные положения Руководства и рекомендации по их применению. В нем дан сравнительный анализ подходов к описанию результатов измерений, принятыми в ГСИ и предлагаемыми в Руководстве, сопоставлены формы представления результатов измерений.

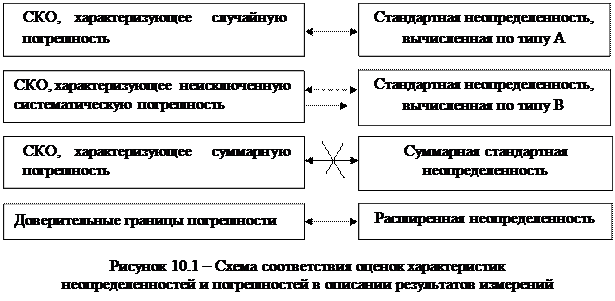
РМГ 43 предлагает применять для сопоставления оценок характеристик неопределенностей и погрешностей результатов измерений схему соответствия (рисунок 10.1). Анализ показывает неполное соответствие, что отражено на схеме. Для оценки СКО, характеризующего неисключенную систематическую погрешность, действительно приходится прибегать к «вычислению неопределенности по типу В», однако оценивание неопределенности по типу В применяют и в других случаях, в том числе и для получения СКО, характеризующего случайную погрешность. В третьей строке «соответствие» кажущееся, оно обусловлено некоторым сходством терминов.

Количественные оценки погрешностей измерений и неопределенностей практически совпадают или различаются незначительно. Проведенные в нормативном документе РМГ 43 расчеты подтверждают, что различия оценок из-за неполного соответствия некоторых алгоритмов расчета и коэффициентов не превышают 11 %, что для рядовых измерений можно считать пренебрежимо малым расхождением.

Из проведенного анализа ясно, что для практического оценивания неопределенности и описания этого процесса можно использовать само «Руководство», его официальный перевод или РМГ 43–2001«Применение "Руководства по представлению неопределенности измерения"»

Дата добавления: 2015-05-26