Сравнение двух случайных выборок (нахождение оценок параметров распределения, проверка статистических гипотез)

Пример

Для иллюстрации методов оптимизации решений в условиях неопределенности рассмотрим упрощенную модель задачи, связанной с оптимизацией выбора способа доставки товара. Пусть некоторая фирма, располагающая свободным капиталом, например, в объеме 800 000$, рассматривает возможность участия в следующей сделке или проекте. Некоторая партия товара (объем партии не подлежит изменению) может быть куплена за 500 000$ и оптово продана за 560 000$. Неопределенность экономического результата связана только с необходимостью доставки товара.

Анализируются следующие способы доставки:

ü Авиатранспорт: стоимость составляет 22 000$, включая страховку по цене приобретения (вероятность авиакатастрофы, по мнению ЛПР, составляет 0,001, но доверия к этому показателю нет, т.е. необходимо реализовать процедуры оптимизации решения в условиях неопределенности);

ü Автотранспорт: стоимость составляет 8 000$, неопределенность обусловлена только возможностью ограбления (вероятность нападения с целью ограбления, по мнению ЛПР, составляет 0,1, но как и в предыдущем случае, доверия к этому показателю нет, т.е. необходимо реализовать процедуры оптимизации решения в условиях неопределенности).

Приведем дополнительные возможности на рынке услуг, которые требуется учесть в рамках анализируемой модели задачи принятия решений в условиях неопределенности.

1. Объявить страховку. Известно, что отношение страхового возмещения к цене страхового полиса составляет 40:1. При этом ЛПР предлагает рассмотреть только два варианта объявления страховки: по цене приобретения и по цене реализации.

2. Нанять охрану. Стоимость составляет 7 000$. Известно, что в 10% случаях наличие охраны не помогает (доверия к этому показателю также нет). Кроме того, ЛПР не будет использовать охрану, если оформляется страховой контракт.

Дополнительно отметим, что при формализации модели известно, что депозитная ставка на период реализации проекта составляет 2%.

ТРЕБУЕТСЯ: найти наилучшее решение, формализовав и решив эту задачу как задачу принятия решений в условиях неопределенности (т.е. в условиях недоверия к предоставленным статистическим данным), - в частности, реализовать следующие процедуры.

1. Составить весь перечень ситуаций, которые влияют на экономические результаты решений, которые необходимо анализировать.

2. Составить перечень анализируемых альтернативных решений.

3. Составить матрицу полезностей.

4. Найти наилучшее решение в рамках каждого из рассмотренных выше соответствующих классических критериев принятия решений в условиях полной неопределенности: ММ -критерий; H -критерий; N -критерий и S -критерий. Кроме того, представить процедуры оптимизации по модифицированному ММ_mod(УТ) -критерию.

ЗАМЕЧАНИЕ. Атрибуты задачи не претендуют на общность. Они упрощены для удобства иллюстрации представленных выше подходов к оптимизации логистических систем в условиях неопределенности.

Решение.

ЭТАПЫ ФОРМАЛИЗАЦИИ МОДЕЛИ

1. Составим весь перечень ситуаций, влияющих на экономические результаты решений, которые требуется анализировать. Предварительно отметим следующее. В ситуации с охраной, когда груз доставляется автотранспортом, нападение с целью ограбления может привести или не привести к потере груза. Это необходимо учесть в структуре матрицы полезностей. Поэтому далее для формализации модели удобно использовать следующую интерпретацию. Считаем, что нападающие могут принадлежать к одной из двух категорий: хорошо организованная группировка - соответственно груз будет потерян, несмотря на наличие охраны; недостаточно организованная группировка - соответственно при наличии охраны груз не будет потерян (при отсутствии охраны он будет потерян). Тогда интересующий нас перечень ситуаций можно синтезировать следующим образом:

Q₁ - {самолет, который мог бы доставлять товар, - долетел} х {машина, которая могла бы доставлять товар, - доезжает без нападения};

Q₂ - {самолет, который мог бы доставлять товар, - долетел} х {на машину, которая могла бы доставлять товар, - напали, но недостаточно организованная группировка};

Q₃ - {самолет, который мог бы доставлять товар, - долетел} х {на машину, которая могла бы доставлять товар, -напали, причем хорошо организованная группировка};

Q₄ - {самолет, который мог бы доставлять товар, - не долетел} х {машина, - которая могла бы доставлять товар, - доезжает без нападения};

Q_s - {самолет, который мог бы доставлять товар, - не долетел} х {на машину, которая могла бы доставлять товар, - напали, но недостаточно организованная группировка};

Q₆ - {самолет, который мог бы доставлять товар, - не долетел} х {на машину, которая могла бы доставлять товар, - напали хорошо организованная группировка}.

2. Составим перечень анализируемых альтернативных решений в формате этой задачи оптимизации в условиях неопределенности с учетом требований ЛПР:

Х₀ - отказаться от участия в сделке и положить деньги на депозит;

Х₁ - вступить в сделку, причем груз доставлять авиатранспортом;

Х₂ - вступить в сделку, причем груз доставлять автотранспортом без использования указанных дополнительных услуг (т.е. без охраны и без объявления страховки);

Х₃ - вступить с сделку, причем груз доставлять автотранспортом, объявляя страховку - по цене приобретения;

Х₄ - вступить в сделку, причем груз доставлять автотранспортом, объявляя страховку - по цене реализации;

Х₅ - вступить в сделку, причем груз доставлять автотранспортом и дополнительно воспользоваться - только услугами охраны

(подчеркнем, что, вообще говоря, возможны и другие решения, но в соответствии с условием далее учитываем, что ЛПР желает рассмотреть именно указанные здесь альтернативы).

3. Для поставленной задачи оптимизации в условиях неопределенности составим соответствующую матрицу полезностей. Для ее атрибутов уже имеем:

• {Q_]; Q₂; Q₃; Q₄; Q_S; Q₆} - перечень возможных ситуаций, влияющих на конечный экономический результат предложения / проекта и образующих соответствующую полую группу случайных событий.

• {Х₀; Х₁; Х₂; Х₃; Х₄; Х₅} - перечень альтернативных решений, которые ЛПР требует анализировать в рамках рассматриваемого предложения / проекта.

Для формализации матрицы полезностей оценим соответствующие показатели конечного экономического результата (дохода) в формате анализируемых решений при указанных выше конкретных внешних ситуациях.

Решение Хо при ситуациях Q₁, Q₂, Q₃, Q₄, Q₅, Q₆:

800.000*(1+0,02)=816.000

Решение Х_] при ситуациях Q_], Q₂, Q₃:

(800.000-500.000-22.000)*1,02+560.000 = 843.560

Решение Х₁ при ситуациях Q₄, Q_s, Q₆:

(800.000-500.000-22.000)*1,02+500.000 = 783.560

Решение Х₂ при ситуациях Q₁, Q₄:

(800.000-500.000-8.000)*1,02+560.000 = 857.840

Решение Х₂ при ситуациях Q₂, Q₃, Q_s, Q₆:

(800.000-500.000-8.000)*1,02 = 297.840

Решение Х₃ при ситуациях Q₁, Q₄:

(800.000-500.000-8.000-12.500)*1,02+560.000 = 845.090

Решение Х₃ при ситуациях Q₂, Q₃, Q_s, Q₆:

(800.000-500.000-8.000-12.500)*1,02+500.000 = 785.090

Решение Х4 при ситуациях Q₁, Q₂, Q₃, Q₄, Q₅, Q₆:

(800.000-500.000-8.000-14.000)*1,02+560.000 = 843.560

Решение Х₅ при ситуациях Q₁, Q₂, Q₄, Q_s:

(800.000-500.000-8.000-7.000)*1,02+560.000 = 850.700

Решение Х₅ при ситуациях Q₃, Q₆:

(800.000-500.000-8.000-7.000)*1,02 = 290.700

Таким образом, матрица полезностей в рамках рассматриваемого здесь условного примера имеет вид, представленный в таблице 10.

Таблица 10

	Q1	Q2	Q3	Q4	Q5	Q6
Х0	816.000	816.000	816.000	816.000	816.000	816.000
Х1	843.560	843.560	843.560	783.560	783.560	783.560
Х2	857.840	297.840	297.840	857.840	297.840	297.840
Х3	845.090	785.090	785.090	845.090	785.090	785.090
Х4	843.560	843.560	843.560	843.560	843.560	843.560
Х5	850.700	850.700	290.700	850.700	850.700	290.700

ЭТАП ВЫБОРА ОПТИМАЛЬНОГО РЕШЕНИЯ

Найдем наилучшее решение применительно к каждому из представленных в этой главе критериев принятия решений в условиях неопределенности.

ММ-критерий:

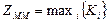, где

Необходимые процедуры выбора наилучшего решения представлены в таблице 11.

Таблица 11

	Q1	Q2	Q3	Q4	Q5	Q6	K
Х0	816.000	816.000	816.000	816.000	816.000	816.000	816.000
Х1	843.560	843.560	843.560	783.560	783.560	783.560	783.560
Х2	857.840	297.840	297.840	297.840	297.840	297.840	297.840
Х3	845.090	785.090	785.090	785.090	785.090	785.090	785.090
Х4	843.560	843.560	843.560	843.560	843.560	843.560	843.560
Х5	850.700	850.700	290.700	850.700	850.700	290.700	290.700

В дополнительном столбце матрицы выделено наилучшее значение показателя К_i для ММ- критерия. Таким образом, в рамках классического ММ -критерия (критерий пессимизма) для данной задачи принятия решений в условиях неопределенности в качестве оптимального будет выбрано решение Х₄. Конечный гарантированный результат дохода составит 843,56 тыс. у.е. Подчеркнем, что при этом ранжирование анализируемых альтернатив (в порядке убывания предпочтения) оказывается следующим:

^Х4, ^Х0, ^Х5, ^Х3, ^Х2, ^Х1.

Отметим, дополнительно, что применительно к рассматриваемому примеру оказалось, что наилучший показатель ММ -критерия достигается именно на одном из анализируемых альтернативных решений. Соответственно, реализация процедур идентификации оптимального решения не требуется. Кроме того, подчеркнем, что указанный выше гарантированный доход (843,56 тыс. у.е.), в частности, реализуется также и в любой из ситуаций Q₁-Q₆.

Н-критерий:

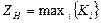, где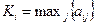

Соответствующие процедуры выбора наилучшего решения представлены в таблице 12.

Таблица 12

	Q1	Q2	Q3	Q4	Q5	Q6	K
Х0	816.000	816.000	816.000	816.000	816.000	816.000	816.000
Х1	843.560	843.560	843.560	783.560	783.560	783.560	843.560
Х2	857.840	297.840	297.840	857.840	297.840	297.840	857.840
Х3	845.090	785.090	785.090	785.090	785.090	785.090	845.090
Х4	843.560	843.560	843.560	843.560	843.560	843.560	843.560
Х5	850.700	850.700	290.700	850.700	850.700	290.700	850.700

В дополнительном столбце матрицы выделено наилучшее значение показателя К_i для Н-критерия. В рамках классического Н-критерия (оптимизма) для данной задачи принятия решений в условиях неопределенности будет выбрано решение Х₂: «вступить в сделку, причем груз доставлять автотранспортом без охраны и без оформления страхового контракта для операций доставки». Естественно, такое решение ориентирует ЛПР на самый благоприятный исход применительно к доставке автотранспортом: события Q₁ и Q₄. Легко видеть, что только в этом случае можно получить соответствующий доход. При этом и ранжирование анализируемых альтернатив соответствует более оптимистической позиции:

X₂, Х₅, Х₃, Х₁ и Х₄, Х₀.

N-критерий:

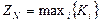, где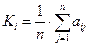

Соответствующие процедуры выбора наилучшего решения представлены в таблице 13.

Таблица 13

	Q1	Q2	Q3	Q4	Q5	Q6	K
Х0	816.000	816.000	816.000	816.000	816.000	816.000	816.000
Х1	843.560	843.560	843.560	783.560	783.560	783.560	613.560
Х2	857.840	297.840	297.840	857.840	297.840	297.840	484.840
Х3	845.090	785.090	785.090	785.090	785.090	785.090	805.090
Х4	843.560	843.560	843.560	843.560	843.560	843.560	843.560
Х5	850.700	850.700	290.700	850.700	850.700	290.700	664.030

В дополнительном столбце матрицы выделено наилучшее значение показателя К _iдля N-критерия. Таким образом, в рамках классического N-критерия (нейтрального критерия) для данной задачи принятия решений в условиях неопределенности будет выбрано именно решение Х₄: «вступить в сделку, причем товар доставлять автотранспортом с объявлением страховки по цене реализации». При этом ранжирование анализируемых альтернатив более соответствует осторожной позиции ЛПР (хотя и отличается от всех предыдущих):

X₄, Х₀, Х₃, Х₅, Х₁, Х₂.

Если, априори считать, что все события полной группы случайных событий Q₁-Q₆ равновозможны (имеют одинаковые вероятности), то указанное решение обеспечит самый большой ожидаемый доход в среднем на одну сделку. Обратим внимание на то, что значение целевой функции критерия, как раз, и указывает на величину такого среднего ожидаемого дохода.

S-критерий:

, где ,

.

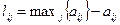Соответствующие процедуры выбора будут представлены ниже. По заданной матрице полезностей в рамках этого критерия сначала надо построить соответствующую матрицу потерь. Для удобства снова представим матрицу полезностей (см. таблицу 14).

Таблица 14

	Q1	Q2	Q3	Q4	Q5	Q6
Х0	816.000	816.000	816.000	816.000	816.000	816.000
Х1	843.560	843.560	843.560	783.560	783.560	783.560
Х2	857.840	297.840	297.840	857.840	297.840	297.840
Х3	845.090	785.090	785.090	845.090	785.090	785.090
Х4	843.560	843.560	843.560	843.560	843.560	843.560
Х5	850.700	850.700	290.700	850.700	850.700	290.700

Здесь в каждом столбце матрицы жирным шрифтом выделено наибольшее значение дохода, которое ЛПР могло бы реализовать при удачном выборе решения из заданного доступного для ЛПР перечня решений. Именно такие доходы (применительно к заданным «внешним» событиям, влияющим на конечный экономический результат) ЛПР могло бы получать, если бы всегда угадывало, какое из событий полной группы наступит. Эти выделенные жирным шрифтом значения возможных доходов определяют утопическую точку, применительно к которой строится матрица потерь для критерия Сэвиджа.

Мы уже отметили, что данный критерий оперирует не с матрицей полезности A=(a_ij), а с матрицей рисков или потерь L= (l_ij). Поэтому от имеющейся матрицы полезностей, т.е. матрицы А, далее переходим к матрице рисков или потерь. Соответствующие потери определяются применительно к каждому элементу исходной матрицы полезностей на основе максимального элемента соответствующего столбца. Другими словами, потери для каждого решения Х_i применительно к каждой ситуации q_j (j= 1,2,...,n) определяются на основе «эталонного» условного решения Х_УТ, параметры которого характеризуют утопическую точку для исходной матрицы полезностей (см. таблицу 15).

Таблица 15

События	Q1	Q2	Q3	Q4	Q5	Q6
Утопический доход при «решении» ХУТ	857.840	850.700	843.560	857.840	850.700	843.560

(именно такие доходы можно было бы реализовать при указанных внешних случайных событиях/ситуациях, если бы заранее знать, какое из них наступит).

Матрица потерь и соответствующие процедуры нахождения оптимального решения на основе такой матрицы представлены в таблице 16.

Таблица 16

	Q1	Q2	Q3	Q4	Q5	Q6	Ki
Х0	41.840	34.700	27.560	41.840	34.700	27.560	41.840
Х1	14.280	7.140		74.280	67.140	60.000	74.280
Х2		552.860	545.720		552.860	545.720	552.860
Х3	12.750	65.610	58.470	12.750	65.610	58.470	65.610
Х4	14.280	7.140		14.280	7.140		14.280
Х5	7.140		552.860	7.140		552.860	552.860

В дополнительном столбце матрицы потерь выделено наилучшее значение показателя К_i для S- критерия. Таким образом, в рамках критерия Сэвиджа для данной задачи принятия решений в условиях неопределенностей будет выбрано решение Х₄: «вступить в сделку, причем товар доставлять автотранспортом с объявлением страховки по цене реализации».

Подчеркнем, что при этом ранжирование анализируемых альтернатив (в порядке убывания предпочтения) оказывается весьма близким к ранжированию по MM-критерию:

X₄, Х₀, Х₃, Х₁, Х₂ и Х₅.

Как видим, оптимальный выбор на основе критерия Сэвиджа оказался таким же, как и в представленных выше случаях ММ-критерия и N-критерия. Но в данной ситуации такой выбор подчеркивает, прежде всего, следующее. При указанном решении самая большая величина возможных потерь будет гарантировано меньшей. А именно, она не превысит 14,280 (тыс. у.е.).

ММ_mod(YT)-критерий:

, где ,

причем ,

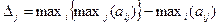
Предварительно, в рамках указанного критерия необходимо выполнить процедуры модификации матрицы полезностей. Для этого применительно к исходной матрице полезностей дописываем две дополнительные строки. А именно:

ü первая - с координатами утопической точки УТ (максимумы по соответствующим столбцам исходной матрицы полезностей);

ü вторая - с показателями требуемых для модификации «добавок» Δ_j к элементам соответствующих столбцов исходной матрицы полезностей (недостачи максимумов по столбцам до максимальной из координат утопической точки, которая выделена далее жирным шрифтом).

Эти процедуры соответственно представлены в таблице 17.

Таблица 17

	Q1	Q2	Q3	Q4	Q5	Q6
Х0	816.000	816.000	816.000	816.000	816.000	816.000
Х1	843.560	843.560	843.560	783.560	783.560	783.560
Х2	857.840	297.840	297.840	857.840	297.840	297.840
Х3	845.090	785.090	785.090	785.090	785.090	785.090
Х4	843.560	843.560	843.560	843.560	843.560	843.560
Х5	850.700	850.700	290.700	850.700	850.700	290.700
УТ	857.840	850.700	843.560	857.840	850.700	843.560
Добавки
Δj		7.140	14.280		7.140	14.280

Теперь можем выписать модифицированную матрицу полезностей, добавляя к каждому элементу исходной матрицы полезностей соответствующую добавку Δ_j, которая указана в том столбце, где и расположен элемент. После этого реализуем процедуры выбора, аналогичные классическому MM-критерию.

Соответствующие процедуры оптимизации решения в условиях неопределенности в формате модифицированного MM_mod(YT) -критерия представлены в таблице 18.

Таблица 18

	Q1	Q2	Q3	Q4	Q5	Q6	Ki
Х0	816.000	823.140	830.280	816.000	823.140	830.280	816.000
Х1	843.560	850.700	857.840	783.560	790.800	797.840	783.560
Х2	857.840	304.980	312.120	877.840	304.980	312.120	304.980
Х3	845.090	792.230	799.370	785.090	792.230	799.370	785.090
Х4	843.560	850.700	857.840	843.560	850.700	857.840	843.560
Х5	850.700	857.840	304.980	850.700	857.840	304.980	304.980

В дополнительном столбце матрицы потерь выделено наилучшее значение показателя K_i для MM_mod(_YT) -критерия. Таким образом, в формате модифицированного MM_mod(YT) - критерия для данной задачи принятия решений в условиях неопределенности (т.е. в условиях, когда имеется недоверие к предоставленным статистическим данным о вероятностях событий Q₁-Q₆) будет выбрано именно решение Х₄: «вступить в сделку, причем товар доставлять автотранспортом с объявлением страховой суммы по цене реализации». Как и следовало ожидать, этот выбор совпал с выбором S-критерия (по матрице потерь Сэвиджа). подчеркнем, что аналогичным образом совпадает и ранжирование анализируемых альтернатив.

Задание для самостоятельного выполнения

Некоторая фирма, располагающая свободным капиталом, в объеме А1 рублей, рассматривает возможность участия в следующей сделке. Некоторая партия товара (объем партии не подлежит изменению) может быть куплена за А2 руб. и оптово продана за А3 руб. Исходные данные к задаче приведены в таблице 20. Неопределенность экономического результата связана только с необходимостью доставки товара.

Анализируются следующие способы доставки:

ü Железнодорожный транспорт: стоимость составляет А4 руб., включая страховку по цене приобретения (вероятность повреждения груза, по мнению ЛПР, составляет 0,1, но доверия к этому показателю нет, т.е. необходимо реализовать процедуры оптимизации решения в условиях неопределенности);

ü Автотранспорт: стоимость составляет А5 руб., неопределенность обусловлена только возможностью дорожно-транспортного происшествия (вероятность ДТП, по мнению ЛПР, составляет 0,003, но доверия к этому показателю нет, т.е. необходимо реализовать процедуры оптимизации решения в условиях неопределенности).

Приведем дополнительные возможности на рынке услуг, которые требуется учесть в рамках анализируемой модели задачи принятия решений в условиях непределенности.

1. Объявить страховку. Известно, что отношение страхового возмещения к цене страхового полиса составляет 40:1. При этом ЛПР предлагает рассмотреть только два варианта объявления страховки: по цене приобретения и по цене реализации.

2. Использовать дополнительную транспортную тару стоимостью А6 руб. для защиты груза в случае «легкого» ДТП. Известно, что в 10% случаях автомобили попадают в ДТП, при которых дополнительная транспортная тара не может обеспечить сохранность груза (доверия к этому показателю также нет). Кроме того, ЛПР не будет использовать дополнительную тару, если оформляется страховой контракт.

Дополнительно отметим, что при формализации модели известно, что депозитная ставка на период реализации проекта составляет 2%.

ТРЕБУЕТСЯ: найти наилучшее решение, формализовав и решив эту задачу как задачу принятия решений в условиях неопределенности - в частности, реализовать следующие процедуры.

1. Составить весь перечень ситуаций, которые влияют на экономические результаты решений, которые необходимо анализировать.

2. Составить перечень анализируемых альтернативных решений.

3. Составить матрицу полезностей.

4. Найти наилучшее решение в рамках каждого из рассмотренных выше соответствующих классических критериев принятия решений в условиях полной неопределенности: ММ -критерий; H -критерий; N -критерий и S -критерий. Кроме того, представить процедуры оптимизации по модифицированному ММ_mod(УТ) -критерию.

Таблица 20

Исходные данные для задачи

№ варианта	А1	А2	А3	А4	А5	А6

Дата добавления: 2015-05-26