Распределение численности безработных по возрастным группам

Задачи для самостоятельного решения

Мода и медиана. Меры вариации.

Практика №2

(см. методические рекомендации стр.4)

Задача 1

Имеется следующее распределе­ние безработных по возрастным группам:

Возрастные группы, лет	Численность безра- ботных, % к итогу
16-19	10,2
20-24	17,9
25-29	12,7
30-49	48,8
50-54	4,0
55-59	4,5
60-72	1,9
Всего	100,0

По данным распределения определить:

1) средний (арифметический) возраст безработных;

2) среднее квадратическое отклонение;

3) коэффициент вариации.

Ответ: 1) = 34,3 года;

2) σ = 11,5 года; 3) V = 33,5%.

Задача 2

Имеются следующие данные за 2005 и 2006 гг. об урожай­ности, посевных площадях и валовом сборе пшеницы (озимой и яровой).

Культура
Урожайность, ц/га	Посевная площадь, млн.га	Урожайность, ц/га	Валовой сбор,млн.ц
Пшеница озимая Пшеница яровая	16,9 10,3	8,2 15,8	17,9 11,0

Определить среднюю урожайность пшеницы: а) в 2005 г. и б) в 2006 г.

О т в е т: а) 12,56 ц/га; б) 13,48 ц/га.

Задача 3

По данным таблицы

Возрастная	Численность безработных, % к итогу
группа	мужчины	женщины
16 - 19 лет	7,7	11,2
20 - 24	17,0	18,5
25 - 29	11,9	11,7
30 - 49	50,9	49,5
50 - 54	4,2	4,0
55-59	5,7	3,8
60-72	2,6	1,3
Итого	100,0	100,0

определить средний возраст безработных: а) мужчин; б) женщин.

Ответ: а) 35,5 года; б) 33,8 года.

Задача 4 (похожая задача будет в контрольной работе)

Имеются следующие данные о распределении семей области по уровню среднегодового дохода.

Среднегодового дохода семьи, тыс. руб.	Численность
семей,
% к итогу
До 200 200-400 400-600 600-800 800-1000 Свыше 1000	15,3
50,6
23,5
7,3
2,2
1,1

Определить в данном распределении:

1) среднегодовой доход семей по области в целом;

2) моду;

3) медиану;

4) среднее квадратическое откло­нение доходов; дисперсию, коэффициент вариации.

5) дециальный коэффициент дифференциации (ДКД) доходов;

6) коэффициент Джини (G).

Ответ: 1) = 367,6 тыс. руб.; 2) Мо = 313,1 тыс. руб.;

3). Me = 337,2 тыс. руб.; 4)σ = 193,8 тыс. руб.;

5) ДКД = 4,7 раза; 6) G= 0,76.

Задача 5

По переписи населения 1926 г. в России доля грамотных среди женщин составляла 46%, а среди мужчин 77%. Определить общий (средний) процент грамотности всего населения и дисперсию этого показателя, если женщины составляли 53% в общей численности населения.

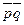О т в е т: 1) = 60,57% (0,6057); 2)σ² = = 0,2388.

Задача 6

В коллективных хозяйствах района средняя урожайность зерновых составила 19 ц/га при среднем квадратическом отклонении 3 ц/га, а в фермерских хозяйствах — соответственно 26 ц/га и 4 ц/га.

Определить:

1) среднюю урожайность зерновых по району, если известно, что посевная площадь под зерновыми в коллективных хо­зяйствах в 9 раз превышает площадь фермерских хозяйств;

2) общую дисперсию и среднее квадратическое отклонение уро­жайности зерновых в районе (по правилу сложения диспер­сии).

О т в е т: 1) = 19,7 ц/га;

2) σ² = ² + δ² = 8,5 + 4,41 = 12,91, σ = 3,6 ц/га.

Задача 7

Для изучения уровня заработной платы рабочих на предприя­тии выборочно обследовано 500 мужчин и 300 женщин. Результаты исследования показали, что у мужчин средняя заработная плата со­ставила 1200 руб. при среднем квадратическом отклонении 200 руб., а у женщин — соответственно 800 руб. и 150 руб.

Определить:

1) общую среднюю заработную плату рабочих на заводе;

2) среднюю из групповых дисперсий;

3) межгрупповую дисперсию;

4) общую дисперсию зарплаты;

5) коэффициент вариации зарплаты на предприятии.

Ответ: 1) = 1050 руб.; 2) = 33 437,5; 3) δ² = 37 500;

4) σ² = 70 937,5; 5) V= 25,4%.

Методические рекомендации для студентов

Задача 1

Определить моду по данным:

Дневная заработная плата, руб.	Число рабочих fi	Середина интер- вала Xi	Xifi
400-500
500-600			11 000
600-700			31 200
700-800			45 000
800-900			35 700
900-1000			19 000
Итого		—	146 400

Для интервального ряда с равными интервалами мода рассчи­тывается по формуле

,

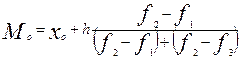где x₀ - начальная (нижняя) граница модального интервала;

h - величина интервала;

f₂ - частота модального интервала;

f₁ - частота интервала, предшествующего модальному;

f₃ - частота интервала, следующего за модальным.

В условии задачи наибольшую частоту (60) имеет интервал (700—800). Отсюда

Мо =700 + 100 (руб.)

т.е. наиболее часто встречается дневная заработная плата в размере 731,6 руб.

В ряду с неравными интервалами мода определяется в интерва­ле, имеющем наибольшую плотность распределения, и в формуле вместо f₁, f₂, f₃, принимаются соответствующие плотности распреде­ления.

Задача 2

Для приведенного в задаче 1 распределения рабочих по разме­ру заработной платы определить медиану.

Перепишем этот ряд и рассчитаем в нем накопленные частоты:

Дневная заработная плата,	Число рабочих	Накопленные частоты
руб.	fi	S
400-500
500-600
600-700
700-800
800-900
900—1000
Итого		—

Для нахождения медианы (значения признака у средней едини­цы ранжированного ряда) сначала определяется ее порядковый номер 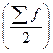, а затем по накопленным частотам определяется либо сама медиана (для дискретных рядов), либо медианный интервал (для интервальных рядов), в котором путем простой интерполяции рас­считывается значение медианы по формуле

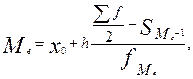
где х₀ — нижняя граница медианного интервала;

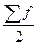— порядковый номер медианы;

— накопленная частота до медианного интервала;

— частота медианного интервала.

Определяем порядковый номер медианы:

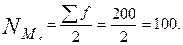
По накопленным частотам видно, что сотая единица находится в интервале (700—800), ее значение определяем по формуле

(руб.),

т.е. делаем вывод по медиане, что половина рабочих получает зара­ботную плату ниже 736,7 руб., а половина — выше.

Примечание. Мода и медиана могут быть определены графически: первая — по гистограмме, а вторая — по кумуляте.

Рассмотрим это на примере.

Построим гистограмму распределения 200 рабочих по размеру заработной платы (рис. 3), для чего на оси абсцисс построим ряд сомкнутых прямоугольников, у каждого из которых основанием слу­жит величина интервала признака (размер заработной платы в руб­лях), а высотой — частота каждого интервала (число рабочих). (Для рядов с неравными интервалами в качестве высоты прямоугольни­ков принимается плотность распределения.)

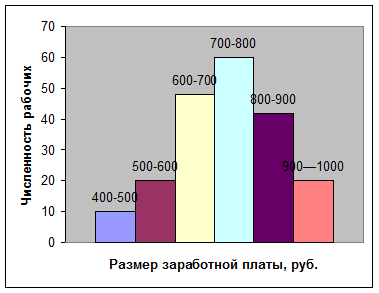
Рис. 3. Гистограмма распределения 200 рабочих по размеру заработной платы (графическое определение моды)

В прямоугольнике, имеющем наибольшую высоту, проводим две линии, как показано на рис. 3, и из точки их пересечения опускаем перпендикуляр на ось абсцисс. Значение х на оси абсцисс в это точке есть мода (Мо).

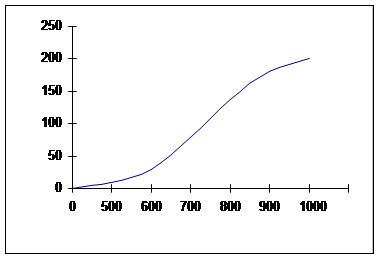
Рис. 4. Кумулята распределения 200 рабочих по размеру заработной платы (графическое определение медианы)

Для графического отыскания медианы по накопленным часто­там строим кумуляту (рис. 4). Для этого из верхней границы каждого интервала на оси абсцисс восстанавливаем перпендикуляр, соответ­ствующий по высоте накопленной частоте с начала ряда по данный интервал. Соединив последовательно вершины перпендикуляров, мы и получим кривую, называемую кумулятой. Из точки на оси ординат, соответствующей половине всех частот (порядковому номеру медианы), проводим прямую, параллельную оси абсцисс, до пересе­чения ее с кумулятой. Опустив из этой точки перпендикуляр на ось абсцисс, находим значение медианы (Me).

Пользуясь кумулятой, можно определить значение признака у любой единицы ранжированного ряда.

Аналогично рассчитываются показатели, именуемые квартиля­ми. Первая квартиль (Q₁) — значение признака у единицы, делящей ранжированный ряд в соотношении 1/4 и 3/4> вторая квартиль равна медиане (Q₂ = Me), третья квартиль (Q₃) — значение признака у еди­ницы, делящей ранжированный ряд в соотношении 3/4 и 1/4. По­рядковый номер Q₁ определяется как Σf/4, для Q₃ — соответствен­но как ³/4 Σf.

Представляет интерес и расчет показателей, именуемых децилями (значение признака у единицы, делящей ранжированный ряд в соотношении 1/10 и 9/10 (первая дециль — D₁), 2/l0 и 8/l0 (вторая дециль — D₂) и т.д.).

Для симметричных распределений характерно совпадение зна­чений средней арифметической, моды и медианы. Если Мо> , то ряд будет иметь левостороннюю асимметрию, а если Мо< , то пра­востороннюю асимметрию. В умеренно асимметричных рядах соот­ношение между указанными показателями выражается следующим образом:

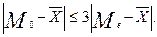
Задача 3

Воспользовавшись исходными данными задачи

Имеется следующее распределение 60 рабочих по тарифному разряду:

Тарифный разряд х.
Число рабочих f.

где =3,9, рассчитаем основные показатели вариации. Расчет оформим в сле­дующей таблице:

xi	fi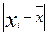
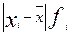
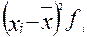
		1,9 0,9 0,1 1,1 2,1	15,2 14,4 1,7 13,2 14,7	28,88 12,96 0,17 14,52 30,87
Σ		—	59,2	87,40

А. Среднее линейное отклонение:

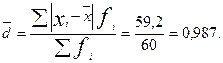
Б. Дисперсия:

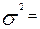
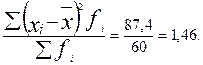
В. Среднее квадратическое отклонение:

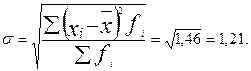
Г. Коэффициент вариации:

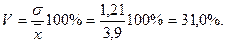
Задача 4

Воспользовавшись исходными данными задачи

Дневная заработная плата, руб.	Число рабочих fi	Середина интер- вала Xi	Xifi
400-500
500-600			11 000
600-700			31 200
700-800			45 000
800-900			35 700
900-1000			19 000
Итого		—	146 400

Рассчитаем среднюю арифметическую, дисперсию и коэффициент вариации, предварительно уменьшив до предела варианты (т.е. способом расче­та от условного нуля):

Середина интервалах.i	Частоты fi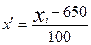
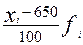
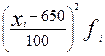
		-2	-20
		-1	-20
Σ		—

1. Средняя арифметическая

= 732 (руб.).

2. Рассчитаем дисперсию. Сначала найдем средний квадрат от­клонений от произвольного числа — в нашем примере от 650, а за­тем скорректируем его на квадрат разности между средней арифме­тической и этим произвольным числом, т.е. применим формулу

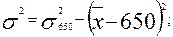
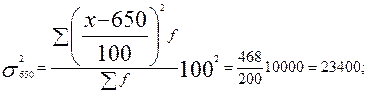
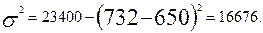
3. Отсюда среднее квадратическое отклонение

.

4. Коэффициент вариации

V= 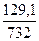100% = 17,6%.

Задача 5

Пусть имеются следующие данные о результатах экзаменацион­ной сессии на I и II курсах одного из вузов: на I курсе 85% студентов сдали сессию без двоек, а на II курсе - 90%. Определить дисперсию доли студентов, успешно сдавших сессию (или, что то же самое, доли студентов, получивших двойки на сессии).

Так как p₁= 0,85 и q₁ = 0,15, а р₂ = 0,9 и q₂ = 0,1, то:

на I курсе σ²₁=p₁q₁ = 0,85 • 0,15 = 0,1275 => σ₁ = 0,35;

на II курсе σ²₂ = р₂ q₂ = 0,9 • 0,1 = 0,09 => σ₂ = 0,3.

Следовательно, на II курсе дисперсия и среднее квадратическое отклонение доли студентов, успешно сдавших сессию, меньше, чем на I курсе.

Задача 6

Имеются следующие данные о распределении семей их 3-х человек по размеру годового денежного дохода. (графы 1,2, 3 табл., ниже см.).

Определить:

1) годовой доход семей с помощью средней арифметической, моды и медианы;

2) среднее квадратическое отклонение годового дохода и ко­эффициент вариации;

3) децильный коэффициент дифференциации доходов;

4) степень концентрации (неравномерности) доходов у отдель­ных семей (коэффициент Джини).

Решение. Необходимые для расчета суммы показаны в таблице.

1. а) Средний годовой доход

= 900,75 (тыс. руб.).

(В качестве весов можно принимать и w_i — относительный по­казатель численности семей в % к итогу. Результат будет тот же.).

Таблица

Годовой доход семьи, тыс. руб.	Численность семей	Середина интервала xi	Суммарный доход по группам xifi	Накоп- ленные частости (доли семей в %) Si=pi	xi^2fi
тыс., fi	%
к итогу,
wi
До 400 400-600 600-800 800-1000 1000-1200 1200-1600 1600-2000 Свыше 2000	25,8 28,7 24,7 19,2 13,8 16,6 8,4 10,3	17,5 19,5 16,7 13,0 9,4 11,2 5,7 7,0	1800.	14 350 17 290 17 280 15 180 23 240 15 120 22 660	17,5 37,0 53,7 66,7 76,1 87,3 93,0	2 322 000 7 175 000 12 103 000 15 552 000 16 698 000 32 536 000 27 216 000 49 852 000
Итого	147,5	100,0	—	132 860	—	163 454 000

б) Мода (наиболее часто встречающийся размер годового дохо­да) находится в интервале 400—600. Определим ее как

= =484 (тыс. руб.),

где х_н — нижняя граница модального интервала.

в) Медиану удобнее находить по данным распределения в %, т.е. по w_i.Тогда порядковый номер медианы равен 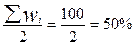. По накопленным частостям определяем, что медиана (50-й процент) находится в интервале 600—800.

Отсюда

Ме= 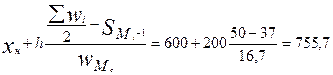(тыс. руб.),

т.е. в июле 1997 г. половина семей имела годовой денежныйдоход ниже 755,7 тыс. руб., а половина — выше 755,7 тыс.

2. а) Среднее квадратическое отклонение найдем по формуле

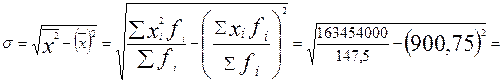
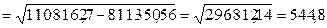(тыс. руб.).

(Можно было использовать и формулу )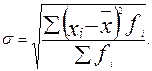

б) Коэффициент вариации

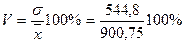= 60%.

Такая вариация весьма значительна, т.е. годовые доходы семей далеко не однородны по размеру.

3. Для оценки степени дифференциации доходов по накоплен­ным частостям (графа 6) определяем, что первая дециль (D₁) нахо­дится в первом интервале (200—400), а девятая дециль (D₉) — в пред­последнем интервале (1600—2000):

a) (тыс.руб.).

D₁ — это максимальный размер годового дохода у десяти процен­тов семей с наименьшими доходами.

Учитывая, что частость первого интервала (17,5%) больше 10% (порядкового номера D₁), расчет D₁ удобнее вести от значения верх­ней границы интервала, вычитая из него величину интервала, при­ходящуюся на излишние 7,5% единиц, т.е.

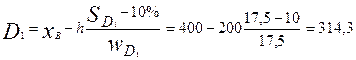(тыс.руб.)

б) = 1600 + 189,5 = 1789,5 (тыс. руб.).

D₉ - это минимальный размер годового дохода у десяти процен­тов семей с наиболее высокими доходами;

в) децильный коэффициент дифференциации {ДКД) доходов

ДКД = = 5,7 (раза).

Примечание. Поскольку в первом интервале не указана нижняя гра­ница, а последующий интервал равен 200 (400—600), то мы вправе и в первом интервале принимать такую же величину, т.е. (200—400).

4. Для расчета коэффициента Джини, G, сначала определяем долю (в %) суммарного дохода по каждой группе как (x_if_i: Σ x_if_i)* 100% (графа 8 в продолжении табл. 1), а затем в графе 9 находим кумулятивные (накопленные) итоги суммарного дохода в % (q_i).

Продолжение табл. 1

Суммарный доход по группам, % к итогу (xifi: Σ xifi)* 100%	Накопленные итоги суммарного дохода, % qi
5,8 10,8 13,0 13,0 11,4 17,5 11,4 17,1	5,8 16,6 29,6 42,6 54,0 71,5 82,9 100,0
100,0	—

По данным граф 6 и 9,

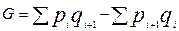= [(17,5*16,6 + 37*29,6 + 53,7*42,6 + 66,7*54 + 76,1*71,5 + 87,3*82,9 + 93*100) - (37,0*5,8 + 53,7*16,6 + 66,7*29,6 + 76,1* *42,6 + 87,3*54 + 93*71,5 + 100*82,9)]: 10 000 = (29253,44 - 25975,9): 10 000 = 0,327 0,33.

По G = 0,33 делаем вывод, что степень концентрации суммар­ных годовых денежных доходов у семей с более высокими доходами сред­няя, не очень высокая.

Задача 7

Имеются следующие условные данные по трем группам рабочих с разным стажем работы:

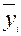
Стаж работы (лет)	Число рабочих пi	Средняя дневная зарплата, руб.	Среднее квадратическое отклонение зарплаты, руб.
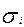
До З 3-10 Более 10

Рассчитать: а) среднюю дневную зарплату для всей совокупности рабо­чих; б) общую дисперсию и среднее квадратическое отклонение зар­платы.

Решение: Общая средняя

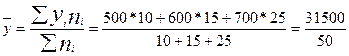= 630 (руб.).

Общая дисперсия находится по правилу сложения дисперсий:

.

Находим среднюю из групповых дисперсий:

.

Межгрупповая дисперсия

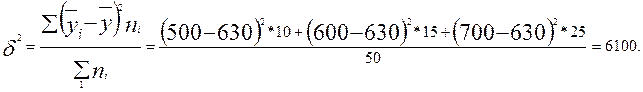Общая дисперсия зарплаты

= 258,8 + 6100 = 6358,8.

Отсюда среднее квадратическое отклонение зарплаты во всей совокупности рабочих

79,7 (руб.).

Примечание. Соотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет оценить его асимметрию. Если , то имеет место правосторонняя асимметрия, при 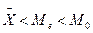следует сделать вывод о левосторонней асимметрии ряда.

Средняя арифметическая часто используется как показатель центра распределения, положительные и отрицательные отклонения от которого индивидуальных значений признака в сумме взаимно погашаются.

Медиана отражает значение признака, сумма отклонений от которого, является наименьшей величиной.

Мода является величиной, вокруг которой группируется наибольшее количество единиц совокупности. При нормальном распределении все эти три показателя имеют одинаковую величину.

Установив значения характеристик центра распределения (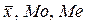), возникает вопрос, в какой мере индивидуальные значения признака отличаются между собой и центральных характеристик от средней. Для этого рассчитываются показатели вариации.

Чем меньше вариация, тем более однородна совокупность и более надежна (типична) средняя величина.

Среднее квадратическое отклонение также, как и среднее линейное отклонение, показывает, на сколько в среднем отклоняются конкретные значения признака от среднего их значения. Среднее квадратическое отклонение всегда больше среднего линейного отклонения.

Среднее линейное отклонение обладает большим преимуществом перед размахом вариации в отношении полноты характеристики колеблемости признака. Однако при этом в некотором смысле нарушается элементарное правило математики, так как отклонения от среднего значения признака складываются без учета знаков.

Среднее квадратическое отклонение измеряет абсолютный размер колеблемости признака и выражается в тех же единицах измерения, что и значения признака (рублях, тоннах, процентах и т. д.). Оно является абсолютной мерой вариации.

Чем больше коэффициент вариации, тем менее однородная совокупность и тем менее типична средняя для данной совокупности. Установлено, в соответствии со свойствами нормального распределения, что совокупность количественно однородна, если коэффициент вариации не превышает 33%.

Дата добавления: 2015-05-26