Правило рычага

Эта стройная теория осложняется множеством факторов. Прежде всего, центр равновесия редко кажется расположенным посередине между двумя объектами — обычно он смещен в сторону того, который кажется нам тяжелее и компактнее (т.е. плотнее). Наиболее динамично и интересно выглядят именно те композиции, в которых баланс достигается не симметричными и равными по плотности группами объектов, а равновесием тяжелого «ядра» и асимметрично расположенной, менее плотной «периферии». Взгляните, к примеру, на рис. 15 на стр. 99:

балансировка здесь происходит по диагонали, так что плотный верхний правый угол уравновешивает весь легкий, разреженный низ композиции. Центр равновесия в данном случае никак не выделен, его положение можно указать лишь приблизительно.

Во многих случаях, напротив, выгодно визуализировать центр баланса, сделать его активным участником компо­зиционных отношений. Для этого достаточно поместить неподалеку от предполагаемого центра баланса некий тре­тий объект, желательно с иным доминирующим аспектом плотности, — центр моментально сместится и «прилипнет» к этому новому объекту. Довольно трудно уловить момент, когда третий объект, удаляясь от исходного центра равно­весия, перестанет перетягивать центр на себя и превратится из «оси» в один из «рычагов» системы.

Рассмотрим небольшой пример. На сайте books.ru (стр. 330) темно-синяя вертикальная полоса слева вводит сильную асимметрию и нуждается в противовесе. Однако поскольку эта полоса занимает лишь около четверти шири­ны всей страницы, противовесу этому совсем не обязательно быть таким же тяжелым, как и сама полоса. Открытое еще Архимедом правило рычага позволяет ограничиться легким горизонтальным разделителем, смещенным к правому краю страницы (рис. 40). Центр равновесия здесь вычисляется совсем не по законам физики; его стягивает на себя гра­ница синего и белого, — т. е. правый край синей полосы, вообще представляющий собой самую сильную вертикаль в композиции.

В этом примере, пожалуй, разумнее говорить не о плот­ности и равновесии цвета вообще, а об отдельном балансе синего, который имеет в этой композиции не центр, а, ско­рее, вертикальную ось равновесия. Второй главный цвет на странице — оранжевый — сбалансирован совсем по-иному: яркий, тяжелый логотип в левом верхнем углу уравнове­шивается несколькими легкими пятнами оранжевых ссылок и заголовков на странице, а также бледной и размытой (и не совсем оранжевой) полосой с фотографией книжной полки. Опять-таки вопреки физическим законам оранжевый круг с черным полумесяцем в логотипе становится в сознании воспринимающего центром «оранжевого равновесия» — и именно поэтому он помещен точно на оси равновесия синего.

Рис. 40

Тяжелая, но ком­пактная темная полоса по ле­вому краю страниц books.ru (пример 15) уравновешивает­ся легкой, но вынесенной дале­ко вправо асимметричной ли­нейкой — разделителем блоков текста (значком 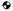на физи­ческих чертежах обозначают центр масс)

В более сложных случаях центры равновесия разных аспек­тов могут не совпадать. При этом смещение по одному аспекту должно компенсироваться противоположным сме­щением по другому, и аспекты эти должны быть как-то свя­заны между собой (как связаны, например, пары контраст­ных цветов или шрифтов). Центр масс «второго порядка», образованный центрами масс разных аспектов композиции, сам может быть расположен достаточно близко к геометри­ческому центру страницы (тогда композиция кажется нам симметричной, хотя бы даже о симметрии в математическом смысле речи не шло) или, наоборот, довольно далеко от него (тогда страница кажется резко асимметричной — но притом все же сбалансированной).

Наконец, при балансировке всей страницы и любого ее участка надо обязательно принимать во внимание силу тяжести — силу, в нашем сознании не менее всемирную, чем в физике (и направленную, разумеется, сверху вниз). Мы уже видели, что центр равновесия композиции логич­но уподобить центру масс тела, — что позволяет понять, почему некоторые композиции кажутся нам легкими и воз­душными (центр масс у них смещен вверх относительно геометрического центра), а другие тяжелыми (центр масс смещен вниз).

Все приведенные выше рассуждения в полной мере отно­сятся и к дизайну веб-страниц. Однако нужно учитывать, что средняя страница не видна в окне броузера вся цели­ком, поэтому сильно разнесенные по вертикали элементы уже не могут взаимодействовать и уравновешивать друг друга. Высоту окна, в котором будет рассматривать вашу страницу пользователь, заранее предсказать невозможно, но вы должны сделать все от вас зависящее, чтобы баланс композиции не нарушался даже при минимальных размерах окна (стр. 193). Частью инстинктивно, частью сознательно большинство веб-дизайнеров решают эту проблему тем, что пользуются горизонтальными отношениями баланса намно­го активнее, чем вертикальными.

Дата добавления: 2015-05-26