Построение лекальных кривых

I-----------------------------,---------------------------,

Рис. 4.4. Сопряжение дуги и прямой заданным радиусом

R, +R

В точке пересечения этих вспомогательных линий получаем центр сопряжения О. Из этого центра О восстанавливаем перпендикуляр на прямую -получаем точку сопряжения на прямой - точку А, затем соединяем центр О с центром дуги Oi - в пересечении прямой 001 с заданной дугой получаем точку сопряжения на дуге - точку В. Между найденными точками А и В радиусом R проводим дугу сопряжения.

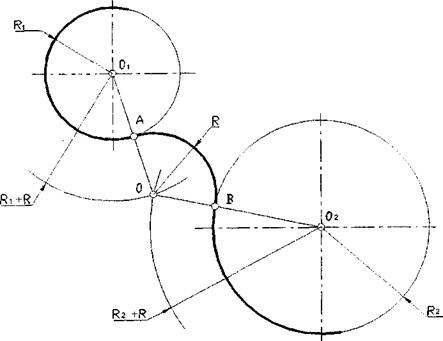
Рис. 4.5. Сопряжение двух дуг заданным радиусом (внешнее касание)

3) Построение сопряжения двух дуг: дуги R, из центра О, и дуги R₂ из центра 0₂. Здесь возможны два варианта: внешнее касание с сопрягающим радиусом (рис. 4.5) и внутреннее (рис. 4.6). К концентрично заданным дугам проводим из центров 0| и 0₂ две вспомогательные дуги радиусами, соответственно равными R_:+ R и R₂+ R, где R - радиус сопряжения, R, и R₂ -радиусы заданных дуг. Точка пересечения вспомогательных дуг определяет центр сопряжения О с центрами заданных дуг 0| и 0₂. Радиусом R проводим дугу сопряжения в пределах точек А и В. Сопряжение двух дуг при заданном радиусе R возможно при следующем условии: 0]0₂ < R, + 2R + R₂.

В случае внутреннего касания построения аналогичны, только радиусы вспомогательных дуг для определения центра сопряжения О определяются как R-R, и R-R₂.

А

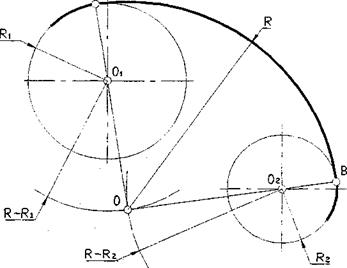
Рис. 4.6. Сопряжение двух дуг заданным радиусом (внутреннее касание)

Рассмотрев наиболее характерные случаи сопряжений при заданном радиусе, можно выявить общее правило построения сопряжений для подобных случаев. Центр сопряжения определяется в пересечении двух вспомогательных линий, параллельных заданным углам и отстоящих от заданных линий на расстояние радиуса сопряжений.

Точки сопряжения определяются: на прямых - перпендикуляром, опущенным из центра сопряжений на прямую; на дугах - прямой, соединяющей центр сопряжений с центром заданной дуги.

4.2.2. Построение сопряжения по заданной точке. Рассмотрим несколько характерных случаев сопряжения двух прямых, прямой и дуги и двух дуг, когда задана точка сопряжения А.

1) Для построения сопряжений двух пересекающихся прямых Ci и С₂ (рис. 4.7) центр сопряжения О определяем в точке пересечения перпендикуляра к прямой С|. проведенного из заданной точки А, и биссектрисы угла, образованного прямыми Cj и С₂. Вторую точку сопряжения В на прямой С₂ определяем с помощью перпендикуляра, опущенного из центра О на прямую С₂. Радиус сопряжения определяем графически: R_x = / OB / = / ОА /.

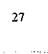
Рис. 4.7. Сопряжение двух прямых в заданной точке

2) Построить сопряжение прямой линии С с дугой радиусом R с центром в точке О. Эта задача может быть решена в двух вариантах: точка А может быть задана на дуге и на прямой. Рассмотрим последовательно оба варианта.

Рис. 4.8. Сопряжение дуги и прямой из точки на дуге

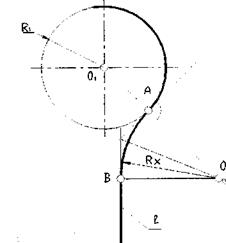а) Точка А задана на дуге. В точке А проводим касательную к дуге. Точка пересечения биссектрисы угла, образованного касательной и заданной прямой С, с продолжением радиуса 0|А определяет центр дуги сопряжения (рис. 4.8). Вторая точка сопряжения В на прямой определяется перпендикуляром, опущенным из точки О на прямую С. Радиус сопряжения R_x определяется графически.

б) Точка А задана на прямой. Из заданной точки А опустить перпендикуляр на прямую С и отложить на нем расстояние, равное R| (рис. 4.9). Полученную точку К соединяем с центром 0|, полученный отрезок 0|К поделим пополам. Центр дуги сопряжения О определяется в точке пересечения перпендикуляра, восстановленного из середины отрезка 0|К и прямой АК. Вторую точку сопряжения В на дуге определяем в точке пересечения прямой 0₍0 с заданной дугой. Радиус сопряжения R_x = ОА = ОВ.

Рис. 4.9. Сопряжение дуги и прямой из точки на прямой

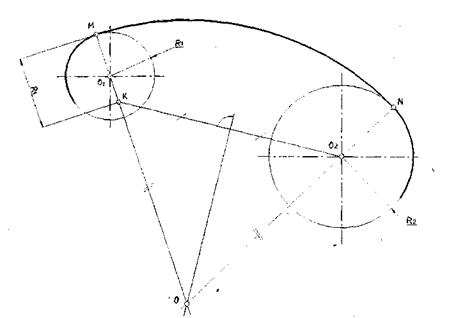
в) Построить сопряжение двух дуг радиусом сопряжения R| из центра сопряжения 0| и радиуса сопряжения R₂ из центра 0₂. Точка сопряжения М задана на дуге, проведенной из центра 0|. Соединяем заданную точку М с центром сопряжения 0| и откладываем на продолжении радиуса 0|М расстояние, равное R₂ (рис. 4.10), от точки М и получаем точку К.

Дальнейшее построение аналогично предыдущему случаю. Полученную точку К соединяем с центром сопряжения 0₂ и делим отрезок К0₂ пополам. Центр дуги сопряжения О определяется в точке пересечения перпендикуляра, восстановленного от середины отрезка КО? и прямой МО]. Вторую точку сопряжения на дуге радиусом R₂ определяем в точке пересечения дуги с прямой 00₂. Радиус сопряжения R_x = ОМ = ON.

При обводке сопряженных линий сначала следует обводить дуги до точек сопряжений, а затем прямолинейные участки.

Рис. 4.10. Сопряжение двух дуг из заданной точки

Лекальные кривые имеют большое применение в технике. Рассмотрим наиболее часто встречающиеся способы построения плоских кривых. Эти кривые обычно обводят с помощью лекал, поэтому они получили название лекальных кривых. Здесь рассматривается построение пяти наиболее распространенных лекальных кривых.

4.3.1. Эллипс. Наиболее часто встречаются резервуары, контуры очертания днища которых имеют форму эллипса (цистерньГи т. д.) (рис. 4.11, а), другой пример, имеющий очертания эллипса, - это эксцентрик (рис. 4.11, б).

Эллипсом называется плоская замкнутая кривая - геометрическое место точек К, сумма расстояний от которых до заданных точек F] и F₂ равняется длине заданного отрезка АВ, проведенного через точки F, и F? так, чтобы отрезок AFi равнялся отрезку BF₂ (рис. 4.12). Отрезок АВ называется большой осью эллипса, а точки F| и F2 - фокусами эллипса. Отрезок СД, проведенный через середину большой оси - точку О - центр эллипса - перпендикулярно к ней, называется малой осью эллипса. Биссектриса смежного с ним угла F|KF₂ называется касательной эллипса. Нормаль перпендикулярна касательной.

Чтобы построить эллипс по двум заданным осям АВ и СД, из центра О (рис. 4.13) эллипса проводят две окружности, диаметры которых равны большой и малой осям эллипса. Из центра эллипса проводят пучок лучей до пересечения с окружностями в точках 1, 2, 3, 4... и Г, 2', 3', 4'.... Из точек 1, 2, 3,4... проводят прямые, параллельные малой оси эллипса, а из точек Г, 2', 3', 4'... - параллельные большой оси. Пересечение соответствующих пар этих прямых определяет ряд точек, соединяя которые плавной кривой получают эллипс.

Для нахождения фокусов F| и F2 надо из точки С как из центра провести дугу радиусом R = АО, она пересечет ось АВ в точках F| и F2 - фокусах.

Рис. 4.13. Построение эллипса

4.3.2. Парабола. Параболой называется плоская кривая, каждая точка которой расположена на одинаковом расстоянии от заданной прямой, носящей название директрисы, и точки, называемой фокусом параболы, расположенных в той же плоскости.

На рис. 4.14 приведен один из способов построения параболы. Даны вершина параболы О, одна из точек параболы А и направление оси - ОС. На отрезке ОС и СА строят прямоугольник, стороны этого прямоугольника-в задании А| и В i-делят на произвольное одинаковое число равных частей и нумеруют точки деления 1, 2, 3, 4,..., 10. Вершину О соединяют с точками деления на А|, а из точек деления отрезка В| проводят прямые, параллельные оси ОС. Пересечения прямых, проходящих через точки с одинаковыми номерами, определяют ряд точек параболы.

Рис. 4.14. Построение параболы

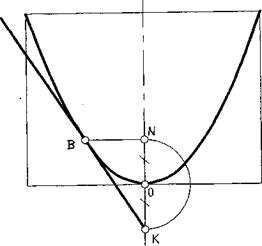
На рис. 4.15 показано построение касательной к параболе в заданной точке В. Касательная соединяет заданную точку В с точкой К, положение которой определяется отношением OK = ON.

Рис. 4.15. Построение касательной к параболе 33

В станкостроении и других отраслях машиностроения часто применяются детали, контурные очертания которых выполнены по параболе, например стойка и рукав радиально-сверлильного станка.

4.3.3.Циклоида. Циклоида - траектория (путь) точки К, лежащей на окружности, которая катится без скольжения по прямой MN (рис. 4.16).

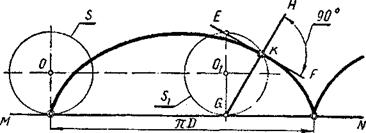
Рис. 4.16. Циклоида

Для ее построения (рис. 4.17) из центра О проводят окружность заданного диаметра и делят ее на несколько равных частей, например на двенадцать. Откладывают вправо от точки К по оси X отрезок КК,₂, равный длине окружности, и делят отложенный отрезок также на двенадцать равных частей (Г, 2', У,..., 12'). Из точек деления отрезка КК₁₂ проводят линии, параллельные оси OY, а из точек 1, 2, 3,..., 11 деления окружности - линии! параллельные оси ОХ.

займет положение, отмеченное точкой К|. После того как окружность перекатится на два деления, ее центр разместится в точке 0₂ над точкой 2', а точка К займет положение, отмеченное точкой К₂, и т. д.

Таким образом, для построения циклоиды из каждого нового положения центра перемещающейся окружности, т. е. из точек Оь 0₂,..., 0|₂ следует описать дугу до пересечения ее с соответствующей линией, проведенной параллельно оси ОХ через точки деления перекатывающейся окружности. В результате получим точки К_ь К₂,..., К,₂, принадлежащие циклоиде. Эти точки следует соединить плавной линией по лекалу.

В качестве примера можно указать на применение циклоиды при вычерчивании контура профиля зубьев некоторых видов реек.

4.3.4. Синусоида. Синусоида - плоская кривая, выражающая закон изменения синуса угла в зависимости от изменения величины угла.

Диапазон изменений величины угла называется длиной волны, или периодом синусоиды. В общем случае длина волны синусоиды равна 2я.

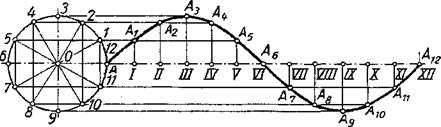
Для построения синусоиды проводят горизонтальную ось и на ней откладывают заданную длину волны АА|₂ (рис. 4.18). Отрезок АА_:2 делят на несколько равных частей, например на 12. Слева вычерчивают окружность радиусом, который равен величине амплитуды, и делят ее на 12 равных частей, точки деления нумеруют и через них проводят горизонтально прямые. Из точек деления отрезка AA_i2 восстанавливают перпендикуляры к оси синусоиды и на их пересечении с горизонтальными прямыми отмечают точки синусоиды. Полученные точки синусоиды А_ь А₂, Аз,..., A_[2 соединяют по лекалу кривой.

Рис. 4.17. Построение циклоиды

Рис. 4.18. Построение синусоиды

До начала перекатывания производящей окружности по прямой КК,₂ точка находится непосредственно под центром окружности. После того как окружность перекатится вправо на одно деление, ее центр переместится из точки О в точку О, и окажется над точкой Г, а исходная точка К, перекатившись на 1/12 часть окружности, поднимется на одно деление вверх и

Чертить синусоиды в технике приходится довольно часто, например, при точном изображении проекций винтовых поверхностей (червяков, лопастей валов винтовых конвейеров, гребных винтов и т. д.), при вычерчивании графиков так называемых гармонических колебательных процессов, кулачков с синусоидальным профилем и пр. (рис. 4.19).

Для построения прямой АВ с заданной величиной уклона к горизонтальной прямой, например 1:4, необходимо отточки А вправо отложить отрезок АС, равный четырем единицам длины, а вверх - отрезок СВ, равный одной единице длины. Точки А и В соединяют прямой АВ, которая дает направление искомого уклона.

По ГОСТ 2.307-68 перед размерным числом, определяющим уклон, наносят условный знак, острый угол которого должен быть направлен в сторону уклона (см. рис. 4.25). Величина уклона может указываться в виде отношения (.например, 1:10) или в процентах (рис. 4.26).

Рис. 4.26. Способы построения полки швеллера

Для построения уклона полки швеллера можно катетами прямоугольного треугольника принять стороны наружного прямого угла профиля (см. рис. 4.26): на нижней полке швеллера откладывают по горизонтали отрезок АВ, равный 100 мм, и по вертикали отрезок АК, равный 10 мм. Через заданную точку С проводят прямую, параллельную КВ.

Другой способ (рис. 4.26): по размерам, указанным в задании, определяют точку С. Из этой точки проводят горизонтальный луч, на котором откладывают отрезок СЕ, равный 50 мм. Из конца отрезка точки Е по вертикали откладывают 5 мм и соединяют точки С и D.

Третий способ (рис. 4.26): строят отдельно в стороне линию MP с заданной величиной уклона 10 % и параллельную MP через точку С прямую уклона.

Уклоны применяются при вычерчивании многих деталей, например, при выполнении чертежей профилей стальных балок и рельсов, изготовляемых на прокатных станах, литьем.

4.5.2. Конусность. Конусностью называется отношение диаметра основания конуса к его высоте (рис. 4.27); обозначается конусность буквой С, Конусность определяется в виде отношения по формуле

С=^, ■

малый диаметр конуса;

где С - конусность; Д - большой диаметр конуса; d L - высота конуса.

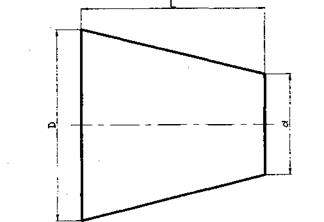
Рис. 4.27. Конусность

По ГОСТ 2.307-68 перед размерным числом, характеризующим конусность, необходимо наносить условный знак конусности, который имеет вид равнобедренного треугольника с вершиной, направленной в сторону вершины конуса (рис. 4.28).

<]Г7

Дата добавления: 2015-05-26