Диференціальне рівняння теплопровідності. Знаходження роз’язку рівняння класичним методом

∂t/∂τ = a ∂²t/∂x². (3.1)

Це рівняння є часткою випадком однорідного диференціального рівняння з постійними коефіцієнтами для деякої функції t від двох змінних x і τ:

(3.2)

Легко перевірити,що частковим розвязком цього рівняннябуде вираз

t = C exp (αx + βτ). (3.3)

Справді:

∂t/∂x = αС ехр (αx + βτ); ∂t/∂τ = βС ехр (αx + βτ);

∂²t/∂x² = α²С ехр (αx + βτ);

∂²t/∂τ² = β²С ехр (αx + βτ); ∂²t/(∂x ∂τ) = αβС ехр (αx + βτ). (3.4)

Спільне вирішення останніх 7 рівнянь дає

a₁α² + b₁αβ + c₁β² + d₁α + l₁β + f₁ = 0. (3.5)

Останнє рівняння називається рівнянням коефіцієнтів.

Переходячи до рівняння (3.1) співставляючи його з рівнянням (3.2), робимо висновок, що b₁ = c₁ = d₁ = f₁ = 0; a₁= - a; l₁ = 1. (3.6)

Рівняння коефіцієнтів (3.5) для часткового випадку рівняння (3.1) отримує вигляд

- α²a + β = 0 (3.7)

или

β = α²a. (3.8)

Таким чином, частковий розвязок (3.3) є інтегралом диференційного рівняння (3.1) і з врахуванням (3.8) матиме вид t = C exp (α²aτ + αx). (3.9)

В в цьому рівняння числа C, α, a можуть приймати будь-які значення.

Вираз (3.9) може бути представлений у вигляді

t = C exp (α²aτ) exp (αx), (3.10)

де співмножник exp (α²aτ) є функцією лише часу τ, а співмножник exp (αx) — тільки відстанні x:

exp (α²aτ) = f (τ); exp (αx) = φ (x). (3.11)

Із збільшенням часу τ температура у всіх точках безперервноросте і може стати вище наперед заданої, що в практичних задачах не зустрічається. Тому зазвичай здебільшого беруть тільки такі значення α, при яких α² відємне.

Приймемо

α = ± iq, (3.12)

де q — довільне дійсне число,

В цьому випадку рівняння (3.10) матиме вид:

t = C exp (- q²aτ) exp (± iqx). (3.13)

Використовуючи формулу Ейлера

exp (± ix) = cos x ± i sin x (3.14)

і, користуючись нею, перетворимо рівняння (3.13). Отримаємо два рішення в комплексному виді:

(3.15)

Підсумовуємо ліві і праві частини рівнянь (3.15), потім відокремимо дійсні від уявних частин в лівій і правій частинах суми і прирівняємо їх відповідно. Тоді отримаємо два рішення:

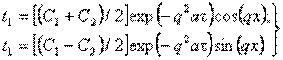(3.16)

Введемо позначення:

(C₁ + C₂)/2 = D; (C₁ - C₂)/2 = C (3.17)

тоді отримаємо два рішення, що задовольняють диференціальному рівнянню теплопровідності (3.1):

t₁ = D exp (- q²aτ) cos (qx); t₂ = C exp (- q²aτ) sin (qx). (3.18)

Відомо, що якщо шукана функція має два приватні рішення, то і сума цих приватних рішень задовольнятиме початковому диференціальному рівнянню (3.1), т. е. рішенням цього рівняння буде

t = C exp (- q²aτ) sin (qx) + D exp (- q²aτ) cos (qx), (3.19)

а загальне рішення, що задовольняє цьому рівнянню, можна записати в наступному виді:

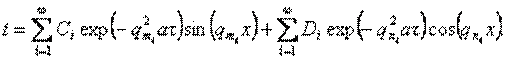
(3.20)

Будь-які значення q_m, q_n, Ci, Di в рівнянні (3.20) задовольнятимуть рівнянню (3.1). Конкретизація у виборі цих значень визначатиметься початковими і граничними умовами кожного приватного практичного завдання, причому значення q_m і q_n визначаються з граничних умов, а C_i, і D_i, — з початкових.

Окрім загального рішення рівняння теплопровідності (3.20) в якому має місце твір двох функцій, одна з яких залежить від x, а інша - від τ, існують ще рішення, в яких таке розділення неможливе, наприклад:

(3.21)

і

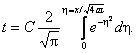
(3.22)

Обидва рішення задовольняють рівнянню теплопровідності, в чому легко переконатися, продиференціювавши їх спочатку по τ, а потім 2 рази по x і підставивши результат в диференціальне рівняння (3.1).

17.Термоелектричне охолодження. Основні параметри роботи термоелектричного холодильника.

При пропусканні електричного струму I через контакт (спай) двох різних речовин (провідників або напівпровідників) на контакті, окрім тепла Джоуля, відбувається виділення додаткового тепла Пельтьє при одному напрямі струму і його поглинання при зворотному напрямі. Це термоелектричне явище називають ефектом Пельтьє. Величина тепла, що виділяється і його знак, залежать від вигляду контактуючих речовин, сили струму і часу його проходження:

.

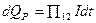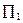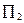Тут - коефіцієнт Пельтье для даного контакту, пов'язаний з абсолютними коефіцієнтами Пельтье і контактуючих матеріалів. При цьому вважається, що струм йде від першого зразка до другого. При виділенні тепла Пельтье маємо: , , 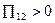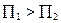. При поглинанні тепло Пельтье вважається негативним і відповідно: 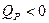, , 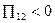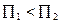. Вочевидь, що . Розмірність коефіцієнта Пельтье [ ] 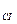=Дж/Кл=В.

Термоелектричний охолоджувальний модуль, як вже зазначалося складається з термоелементів, які ще називають термопарою, або термопарним елементом (рис.1.). Фактично такий термоелемент – найпростіша конструкція термоелектричного охолоджувача, тому розглянемо модель термоелемента.

Рис. 1. Термопарний елемент:1,2-вітки n і p- типу провідності,

3-комутаційна перемичка.

Класичний термоелемент складається з двох термовіток, які електрично з’єднані між собою за допомогою комутаційних пластинок. Термовітки виготовлені з термоелектричних матеріалів: один 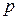, а другий – типу провідності. При температурі на спаях ,через термопару пропускається струм, протилежний її термоЕРС і це дозволяє розглядати термопару як найпростішу термоелектричну холодильну установку. Згідно з термодинамікою,на холодному спаї кожну секунду поглинається тепло , а на гарячому виділяється 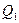. При чому, вважається, що вітки термопари адіабатично ізольовані і теплообмін відбувається тільки на спаях. Тому

, (1.8)

де W – потужність струму.

Вирази для потоків тепла на теплопоглинаючих „холодних” і тепловиділяючих „гарячих” спаях термопарного елемента мають вигляд:

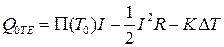, (1.9)

, (1.10)

де , = - , , , , 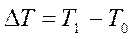Т₁ і Т₀ – температури гарячих і холодних спаїв, І – електричний струм, Π – коефіцієнт Пельтьє, 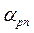- диференційна термоЕРС, R і K – електричний опір і теплопровідність термоелемента, ρ і k – питомий електричний опір і коефіцієнт теплопровідності матеріалу віток, r_c – опір одиниці площі контакту вітки, S, l – площа перерізу та висота вітки, де індекси n і p відносяться до віток n і p типів відповідно.

Споживана термоелементом електрична потужність W знаходиться у відповідності з першим началом термодинаміки, як різниця:

. (1.11)

Найважливішим показником роботи охолоджувача, що характеризує його енергетичну ефективність, є холодильний коефіцієнт, який визначається як відношення:

, (1.12)

Дата добавления: 2015-05-26