Кинематика поступательного движения

Тема 1. Кинематика поступательного и вращательного движения.

ЧАСТЬ I. Механика

КОНСПЕКТ ЛЕКЦИЙ по физике

Учебно-методическое пособие

(для всех специальностей)

Ростов-на-Дону

УДК 531.383

Учебно-методическое пособие. Конспект лекций по физике (для всех специальностей). – Ростов н/Д: Рост. гос. строит. ун-т, 2012. – 103 с.

Содержится конспект лекций по физике, основанный на учебном пособии Т.И. Трофимовой «Курс физики» (изд-во Высшая школа).

Состоит из четырех частей:

I. Механика.

II. Молекулярная физика и термодинамика.

III. Электричество и магнетизм.

IV. Волновая и квантовая оптика.

Предназначено для преподавателей и студентов в качестве теоретического сопровождения лекций, практических и лабораторных занятий с целью достижения более глубокого усвоения основных понятий и законов физики.

Рекомендуется для самостоятельной работы студентов всех специальностей очной и заочной формы обучения.

УДК 531.383

Составители: проф. Н.Н.Харабаев

доц. Е.В.Чебанова

проф. А.Н. Павлов

Редактор Н.Е.Гладких

Темплан 2012 г., поз. Подписано в печать

Формат 60х84 1/16. Бумага писчая. Ризограф. Уч.-изд.л. 4,0.

Тираж 100 экз. Заказ

_________________________________________________________

Редакционно-издательский центр

Ростовского государственного строительного университета

334022, Ростов-на-Дону, ул. Социалистическая, 162

© Ростовский государственный

строительный университет, 2012

Положение материальной точки А в декартовой системе координат в данный момент времени определяется тремя координатами x, y и z или радиусом-вектором – вектором, проведенным из начала системы координат в данную точку (рис. 1).

Движение материальной точки определяется в скалярном виде кинематическими уравнениями: x = x(t), у = y(t), z = z(t),

или в векторном виде уравнением: .

Траектория движения материальной точки – линия, описываемая этой точкой при её движении в пространстве. В зависимости от формы траектории движение может быть прямолинейным или криволинейным.

Материальная точка, двигаясь по произвольной траектории, за малый промежуток времени D t переместиться из положения А в положение В, пройдя при этом путь D s, равный длине участка траектории АВ (рис. 2).

A

Рис. 1 Рис. 2

Вектор , проведенный из начального положения движущейся точки в момент времени t в конечное положение точки в момент времени(t+ D t), называется перемещением, то есть .

Вектором средней скорости называется отношение перемещения к промежутку времени D t, за который это перемещение произошло:

.

Направление вектора средней скорости совпадает с направлением вектора перемещения .

Мгновенной скоростью (скоростью движения в момент времени t) называется предел отношения перемещения к промежутку времени D t, за который это перемещение произошло, при стремлении D t к нулю: = ℓim_Δt→0Δ 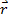/Δt = d 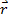/dt =

Вектор мгновенной скорости направлен по касательной, проведенной в данной точке к траектории в сторону движения. При стремлении промежутка времени D t к нулю модуль вектора перемещения стремится к величине пути D s, поэтому модуль вектора v может быть определен через путь D s: v = ℓim_Δt→0Δs/Δt = ds/dt =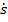

Если скорость движения точки со временем изменяется, то быстрота изменения скорости движения точки характеризуется ускорением.

Средним ускорением ‹a› в интервале времени от t до (t + D t) называется векторная величина, равная отношению изменения скорости () к промежутку времени D t, за который это изменение произошло: 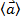= Δ /Δt

Мгновенным ускорением или ускорением движения точки в момент времени t называется предел отношения изменения скорости к промежутку времени D t, за который это изменение произошло, при стремлении D t к нулю:

,

где – первая производная от функции по времени t,

– вторая производная от функции по времени t.

Эти производные принято обозначать соответственно в виде: и .

Вектор ускорения может быть разложен на две составляющие:тангенциальную и нормальную , то есть:

.

Тангенциальная составляющая определяет быстроту изменения модуля скорости : .

Вектор направлен по касательной к траектории движения и для ускоренного движения совпадает с направлением вектора скорости , а для замедленного движения – противоположен вектору скорости .

Нормальная составляющая определяет быстроту изменения направления скорости v: a_n = v²/r, где r – радиус кривизны траектории движения.

Вектор направлен по нормали к траектории движения к центру ее кривизны (поэтому нормальную составляющую ускорения называют также центростремительным ускорением).

Дата добавления: 2015-05-26