Универсальная тригонометрическая подстановка

Универсальная тригонометрическая подстановка – это частый случай метода замены переменной. Её можно попробовать применить, когда «не знаешь, что делать». Но на самом деле есть некоторые ориентиры для ее применения. Типичными интегралами, где нужно применить универсальную тригонометрическую подстановку, являются следующие интегралы: , , 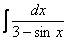, 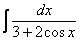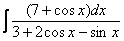и т.д.

Пример 1

Найти неопределенный интеграл.

Универсальная тригонометрическая подстановка в данном случае реализуется следующим способом. Проведем замену: .

Здесь удобнее находить дифференциал , для этого из равенства , я выражаю :
Навешиваю на обе части арктангенс:

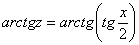
Арктангенс и тангенс взаимно уничтожаются:

Таким образом:

Выражение справедливо только в том случае, если под синусами и косинусами у нас просто «иксы», для интеграла (о котором мы еще поговорим) всё будет несколько иначе!

При замене синусы и косинусы у нас превращаются в следующие дроби:
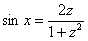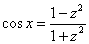, , эти равенства основаны на известных тригонометрических формулах: ,

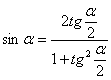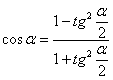
Итак:

Проведем универсальную тригонометрическую подстановку:

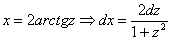
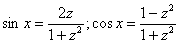
(1) Производим в исходный интеграл подстановку: , , .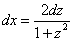

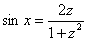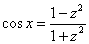(2) Приводим знаменатель к общему знаменателю.

(3) Избавляемся от четырехэтажности дроби, при этом 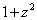у нас сокращается. Раскрываем скобки в знаменателе, двойку в числителе выносим за знак интеграла.

(4) Приводим подобные слагаемые в знаменателе.

(5) Интеграл 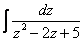решается методом выделения полного квадрата

(6) Выделяем полный квадрат и готовим интеграл для интегрирования.

(7) Интегрируем по табличной формуле .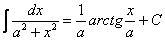

(8) Проводим обратную замену, вспоминая, что .

Готово.

Пример 2

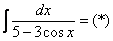
Проведем универсальную тригонометрическую подстановку:

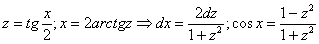
Пример 3

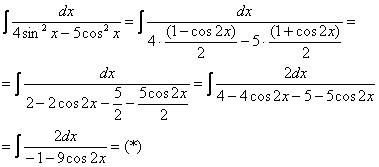
Универсальная тригонометрическая подстановка:

Рассмотрим похожий интеграл:

Здесь тоже проводится универсальная тригонометрическая подстановка: .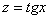
Обратите внимание, что аргумент под тангенсом должен быть в два раза меньше, чем под синусом и косинусом. Формулы 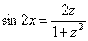, сохраняют статус-кво, а вот дифференциал будет немного другой

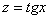
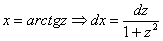
Интеграл 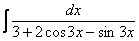решается путем замены 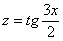и т.д., всё точно так же, единственное отличие, дифференциал будет опять немного другой.

Некоторые формулы: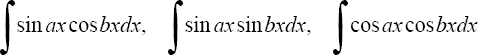

находятся с помощью тригонометрических формул

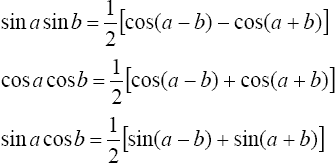
где m и n - четные числа находятся с помощью формул понижения степени

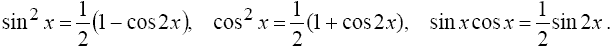
Если хотя бы одно из чисел m или n - нечетное, то полагают (пусть m = 2k + 1)

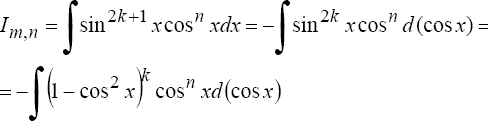
Дата добавления: 2015-05-26