Использование частотных распределений

Для того чтобы понять, насколько различаются условия, мы можем нанести частотные распределения для этих условий на один и тот же график. Сравнение становится более понятным, если не только отмечать высоту колонок, но соединить их вершины линией. (Это называется полигоном частот.) Данный метод уже был показан на рис. 4.3 для эксперимента по обучению испанскому языку.

По значительному перекрытию распределений мы можем судить, что тестовые оценки для двух условий — письменного и устного — различались незначительно.

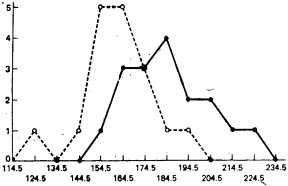
Рассмотрим теперь распределения для эксперимента по измерению времени реакции, описанного в статистическом приложении к главе 1. Они показаны на рис. 4.4. Напомним, что это вымышленные данные. Предположим теперь, что они были получены в межгрупповом эксперименте. Тогда каждый из показателей времени реакции представляет среднее для одного из испытуемых, где 17 испытуемым предъявлялось данное условие. Этот пример может быть с тем же успехом представлен в терминах интраиндивидуального эксперимента, как он первоначально излагался. Рассмотрение эксперимента как межгруппового мы делаем только для того, чтобы связать наш анализ с тематикой данной главы.Видно, что в данном случае различия между условиями более отчетливы, чем в эксперименте с испанским языком, т. е. перекрытие между распределениями меньше. Было бы хорошо иметь количественную меру различия вместо таких неопределенных терминов, как «кажется», «очевидно» и т. д. Такая количественная мера давала бы информацию, насколько сильна связь между независимой и зависимой переменными.

ВЫЧИСЛЕНИЕ ω²

Мы можем получить численную величину силы связи, вычислив ω² (ω — малая греческая буква омега; мы называем ω² омегой в квадрате). По существу, ω² — один из параметров генеральной совокупности, о которых рассказывалось в статистическом приложении к главе 1. Его полное описание можно найти в работе Хейса (1973).

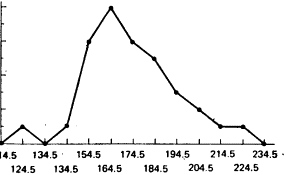
Рис. 4.4.Частотное распределение средних значений времени реакции на световой (условие А) и звуковой (условие Б) сигналы. Ось абсцисс — средние значения времени реакции (в мс). ось ординат — частота. Сплошная линия — световой сигнал, пунктирная — звуковой	Рис. 4.5.Объединенное частотное распределение средних значений Семени реакции. Ось абсцисс — средние значения времени реакции (в мс). Ось ординат — частота

Наше вычисление с использованием данных по выборке испытуемых дает оценку ω². Мы будем называть ее est ω².Давайте построим новый график результатов эксперимента по измерению времени реакции. Однако теперь мы не будем делать различий между тем, какое из двух условий — А (свет) или Б (тон) —было использовано. Как видно на рис. 4.5, это комбинированное распределение несколько более растянуто, чем каждое из отдельных распределений для света и тона. Чем больше исходные распределения отличаются друг от друга, тем больше будет растянуто комбинированное распределение.Если бы мы смогли провести бесконечный эксперимент и при этом получили бы распределения, показанные на рис. 4.4 и 4.5, мы могли бы вычислить ω² прямо из параметра σ̅² _X следующим образом:

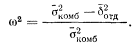
(4.1)Однако поскольку наши данные получены только по одной выборке испытуемых, а не в бесконечном эксперименте, мы должны оценивать ω² по статистике S²_X:

(4.2)Квадрат стандартного отклонения распределения называется дисперсией. Числитель этой формулы дает разность между дисперсиями комбинированного распределения и отдельного распределения, в нашем случае любого из условий А или Б. Делением этой разности на дисперсию комбинированного распределения мы придаем ей форму пропорции. Она отвечает на вопрос, на какую часть уменьшается дисперсия показателей при переходе от комбинированного распределения к отдельному.Производя вычисления, нет необходимости сначала вычислять S_X и затем возводить его в квадрат, чтобы получить S²_X. Вспомните (из формулы 2.2):

Поэтому

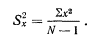
(4.3)

В статистическом приложении к главе 3 мы вычислили ∑ х² для условия А (свет) и условия Б (тон):

Используем эти величины для нахождения S²_отд. Согласно Хейсу (с. 418), среднее по S²_A и S²_Б дает величину S²_отд при допущении равенства «истинных» дисперсий двух наборов:

(4.4)

поэтому

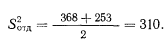
Такое же вычисление производится для комбинированного распределения:

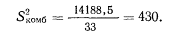
Подставляя эти величины в формулу 4.2, получаем

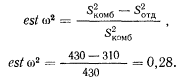
Это показывает сильную связь между независимой и зависимой переменными. Даже значение 0,20 уже достаточно существенно. Значение никогда не может превысить 1; однако эта величина достигается редко. В то же время вычисление для эксперимента с испанским ЯЗЫКОМ дает

Это очень слабая связь между независимой и зависимой переменными.

ПРИМЕНЕНИЯ ω²

Обратите внимание, что для S² _отд необходимо допускать равенство истинных дисперсий для двух условий. В эксперименте по измерению времени реакции это допущение было приемлемым, поскольку дисперсии для двух условий довольно близки по величине. Это справедливо и для эксперимента с испанским языком. Однако для эксперимента с информацией о ценах (см. табл. 4.1) условие В давало значительно меньшее стандартное отклонение (особенно для времени выбора покупки), чем другие условия. Три дисперсии (квадраты стандартных отклонений) были равны 100, 92 и 1,2 для условий А, Б и В. При столь значительном различии прямого способа вычисления ω2 нет. И здесь дело не в том, что число условий равно трем, а не двум. Если значения дисперсии близки, то величина ω² может быть вычислена для любого числа условий с использованием S² _отд как среднего значения для всех условий. Приводившаяся процедура вычисления ω² может быть использована как для интраиндивидуальных, так и для межгрупповых данных. Дисперсия — это то, что относится к пробам, а не к испытуемым.

ИНТЕРПРЕТАЦИЯ ω² Мы можем рассматривать ω² как индикатор величины, на которую уменьшается неопределенность за счет того, что нам известно экспериментальное условие. В эксперименте по измерению времени реакции мы кое-что знаем о среднем показателе для каждого отдельного испытуемого благодаря тому, что знаем экспериментальное условие. Но в пределах каждого условия показатели варьируют, т.е. как-то распределены. Наша неопределенность измеряется дисперсией этого распределения. Если мы не знаем условия, предъявлявшегося испытуемому, наша неопределенность увеличивается: дисперсия комбинированного распределения больше, чем дисперсия для отдельного условия.Таким образом, зная, какое из условий предъявляется испытуемому, мы уменьшаем неопределенность. Как уже говорилось, деление этого уменьшения на уменьшаемую дисперсию (S² _комб) превращает ответ в отношение. Тем самым ω² сообщает нам часть, на которую уменьшается неопределенность при знании экспериментального условия. Это и есть мера воздействия на поведение независимой переменной. Задача: Вычислите est ω² для эксперимента, сравнивающего условие В и Г, с 18 испытуемыми в каждой группе:

∑x²в=4700; ∑x²г=4900; ∑x²комб=15,000.

Ответ: est ω²=0,34.

Глава 5. ВЫДЕЛЕНИЕ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ

Дата добавления: 2015-05-26